この記事でわかること
・コア形状とサイズの選定
・インダクタンスと巻き数の算出法
・ギャップ長、巻線の線径の決め方
スイッチング電源で使用するトランスは、電源毎に仕様が異なる事から、
他の部品のように標準品として販売されていないため、
メーカーに仕様を提示し、カスタム品を製作してもらうことになります。
しかし、試作段階では、仕様や回路の変更が発生するため、
その度にメーカーに依頼していてはコストや時間がかかってしまいます。
このため、回路設計者がトランスを設計し、試作できるようにする必要があります。
試作方法については下記記事で解説しています。
本記事では、少電力(数十W程度)の小型電源として、回路の内部電源等に利用される
フライバック・コンバータのトランス設計方法について解説します。
トランス設計手順
以下の順番でトランスの各種仕様を決めていきます。
1.コアの選定
2.一次側ピーク電流Ip
3.一次側インダクタンスLp
4.一次側巻き数Np
5.コアのギャップ長ℓg
6.二次側巻き数Ns
7.巻線の線径
ここでは、以下に示す他励式フライバック・コンバータに使用するトランスを例にします。
(以下、フライバック電源と称します)
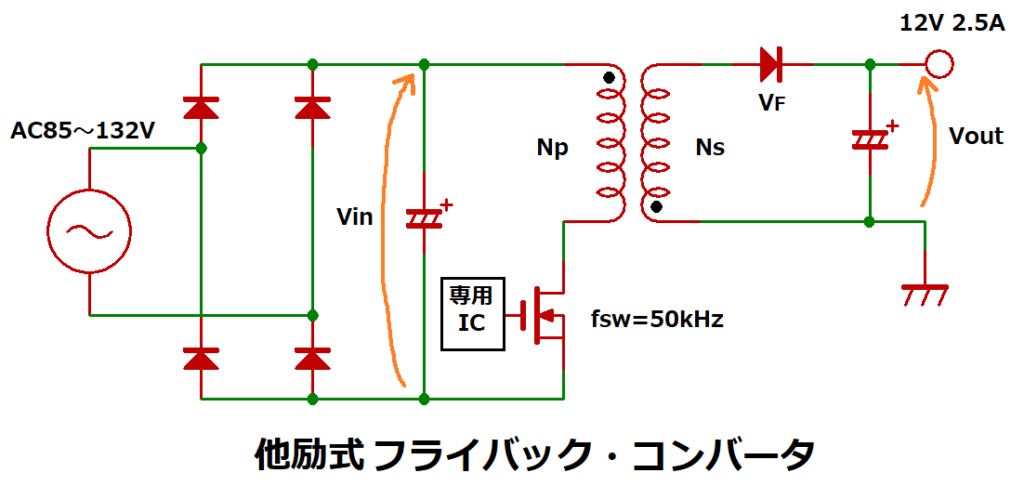
・電源仕様
入力:AC85~132V 50/60Hz
出力:DC12V/2.5A (30W)
スイッチング周波数:50kHz
効率:85%
コアサイズの選定
コアが対応できる出力電力は、コアの断面積と巻枠の面積で決まります。
出力電力 ∝ コアの実効断面積Ae × 巻線断面積Acw
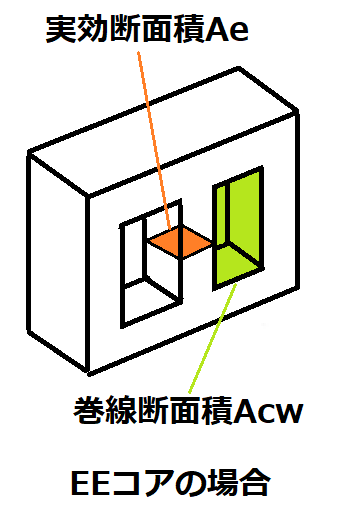
AeとAcwが大きいと太い電線を巻けるので、大電流を流すことができます。
以下に出力電力とコアサイズの目安を示します。
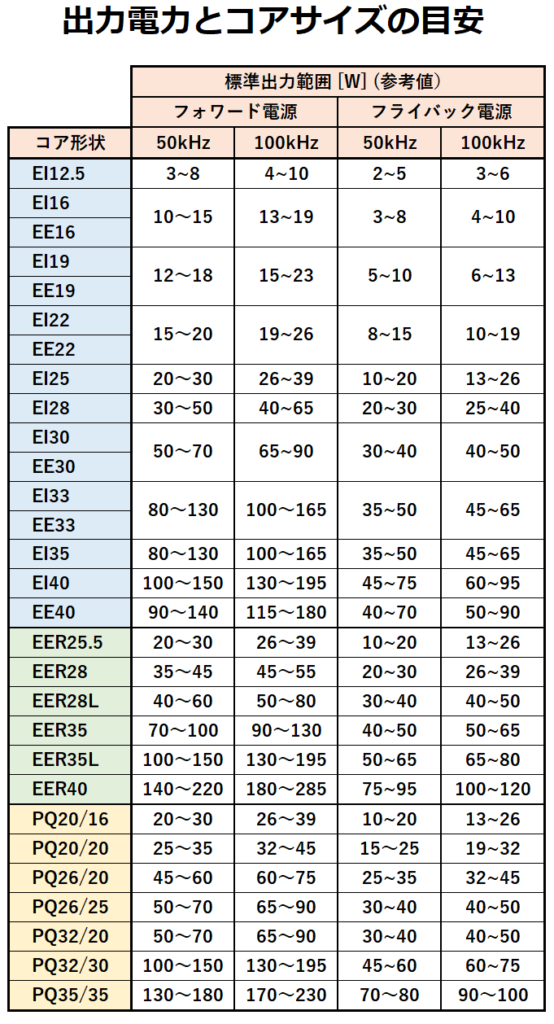
表にあるコア形状はスイッチング電源でよく利用されるものです。
EI、EE :安価だが巻線脚が矩形なので巻き難い
EER:巻線脚が円形のため巻き易いことから、最も良く使われる
PQ :磁気回路的に無駄が無く理想的な形状で、軽量化できる

スイッチング周波数はフライバック電源では通常、50kHz~100kHzの範囲で動作するため、
この表では、2つの周波数における出力電力が記載されています。
理論上は、スイッチング周波数が倍になれば、出力電力も倍になる筈ですが、
FETのスイッチング損失が増えるため、実際の出力電力は表のように
50kHz→100kHzにした場合、1.2~1.3倍程度となります。
本例の出力電力は30Wなので、EER28Lを選定します。
理想的にはPQコアが良いのですが、EERの方が巻き易く、安価なので試作に向いています。
コア材質の選定
抵抗に電流を流すことで、抵抗に電圧が発生するのと同様に、
コアに磁界Hを加えることで、コア内に磁束Φが発生します。
磁界Hはコアに巻いた電線に電流を流すことで発生します。
磁束Φとは磁力線の本数であり、この本数が多い程、磁力が大きく強い磁石と言えます。
コア材の性能を占めす指標として使われる磁束密度Bは、
コアの単位面積あたりの磁束(Φ=B・Ae)であることから、Bは大きい方が望ましいです。
このBとHの関係を示すB-H曲線において、
フライバック電源はコアに流す電流が一方向なので、
Hは+の範囲でしか移動しません。
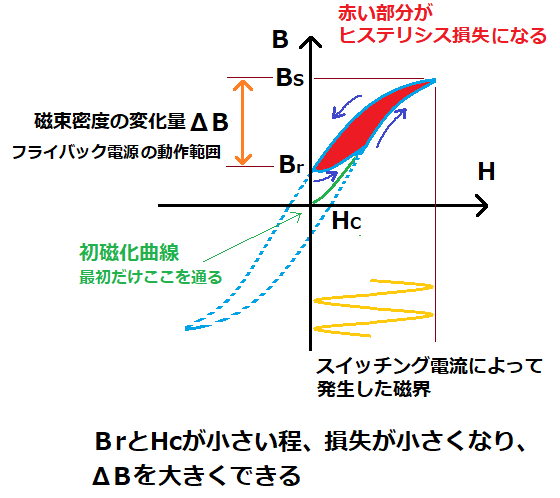
このため、電源動作時、Bは図に示すようなループ上を移動します。
このとき、コアの特性上、Hがゼロ(つまり、電流ゼロ)でもBはゼロになりません。
これを残留磁束密度Brと呼びます。
また、Hを増やしても、Bが増えなくなる限界を飽和磁束密度Bsと呼びます。
従って、磁束密度BはBsとBrの間で変化し、
この変化量ΔB=BsーBrが大きい程、大きな電力を伝えることができます。
また、コアで発生するヒステリシス損失は、B-H曲線が囲む面積に相当するため、
保持力Hcと残留磁束密度Brが小さい方がロスが少なく良い材質と言えます。
本例では、TDK製スイッチング電源用フェライトコアPC95を選定しました。

一次側ピーク電流Ip
一次巻線に流れるピーク電流Ipを求めます。
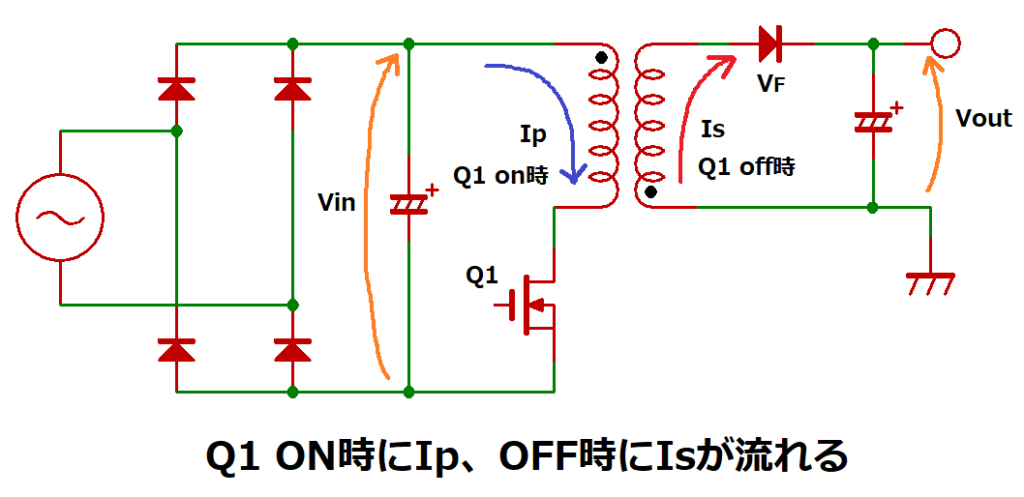
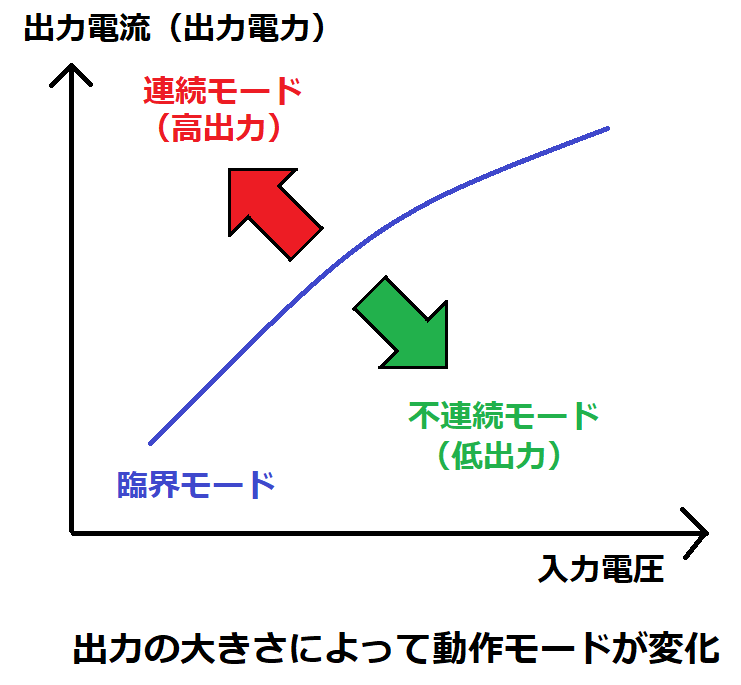
他励式フライバック電源は、入力電圧と出力電流の状態によって、
3つの動作モード(不連続、臨界、連続)があり、Ipの算出式が異なります。
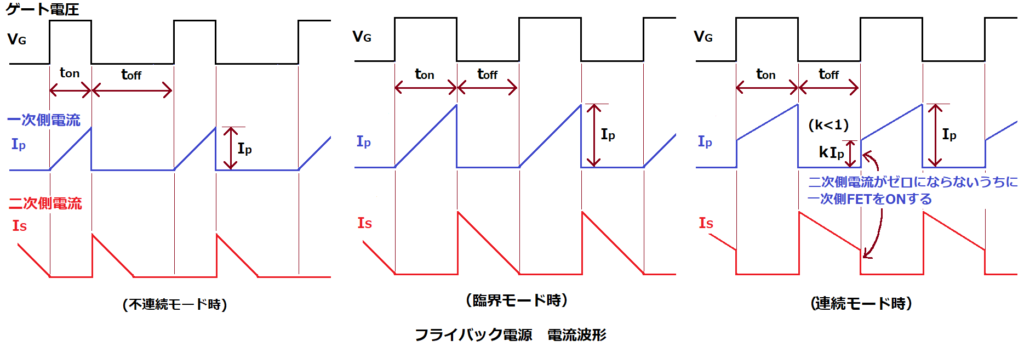

P:出力電力 [W]
T:スイッチング周期 [s]=1/SW周波数 [Hz]
η:効率 [%]
本例では85%にしていますが、複数の2次側出力や、5A以上の大電流、
ワールドワイド入力(AC85~264V)対応などの場合は効率を75%程度まで下げておきます。
Vin:入力電圧の最小値 [V]
AC入力の場合、ブリッジダイオードで全波整流後、コンデンサで平滑されたDC入力電圧になります。
この時、DC電圧はACリップル成分があるので、その下限値とします。
目安としては、AC波形のピーク値(実効値×√2)の90%程度です。
本例のAC85Vでは、85×√2×0.9=108Vとなります。
ブリッジ整流回路のリップル電圧の算出については下記記事で解説しています。
ton:スイッチングON時間 [s]=T×D(ON DUTY [%])
一次側FETスイッチング時のON時間で、スイッチング周期に対するON時間の割合を
ON DUTY (D) と呼び、通常、最低入力電圧時に最大出力となるD=0.5にします。
本例の50kHzでは、T=20us、ton=T×D=20×0.5=10usとなります。
k:ピーク電流Ipに対する直流成分の割合(k<1)
kを大きくすれば、コイルに流れるピーク電流Ipが小さくなるので、
磁気飽和(後で説明)しにくくなり、大電力を扱いやすくなります。
kが未定の場合は、まずはk=0(臨界モード)で設計し、低出力電流で動作させ、
徐々に出力を上げていき、波形やノイズ、効率等を測定しながら、kを調整していきます。
<計算例>
本例では、最大出力(最小入力電圧で最大出力電流)時に
臨界モードで動作させた場合のIpを求めます。
Ip=2・P・T/( η・Vin・ton)
=2 × 30 × 20 × 10-6/(0.85 × 108 × 10 × 10-6)
≒1.3 [A]
<参考:(1),(2)式になる理由>
一次側電流波形は三角波なので、仮にON DUTYが100%とした場合、平均値は以下の式となります。
Iin(ave) =Ip/2
ON DUTY (D)の割合だけ平均値が下がるので、
Iin(ave) =(Ip/2)・D=(Ip/2)・(ton/T)
以上から、出力電力Pは以下の様になります。
P=Vin・Iin(ave)・η
=Vin・[(Ip/2)・(ton/T)]・η
式を変形すると(1)式になります。
Ip=2・P・T/( η・Vin・ton)
連続モードの場合は、
Iin(ave) =kIp+(1-k) Ip/2=(1+k)Ip/2なので、
P=Vin・[((1+k)Ip/2)・(ton/T)]・η となり、
変形すると(2)式になります。
Ip=2・P・T/[( η・Vin・ton)(1+k)]
<参考:磁気飽和について>
磁気飽和とは、電流を多く流すとインダクタンスLが低下してしまう現象で、
コイルとして機能しなくなる(ただの電線と同じになる)ことで、回路がショートする恐れがあります。
磁気飽和が発生する仕組みは以下の通りです。
L=N・Φ/I=N・B・Ae/Iより、
巻き数Nと断面積はAeは固定値なので、
インダクタンスLは磁束密度Bに比例し、電流Iに反比例します。
このため、先程のB-H曲線より、Iがある程度増加するとBが増えなくなので、Lが低下します。
コイルのインピーダンスは2・π・fs・Lです。(fsはスイッチング周波数)
Lが減少するとインピーダンスが低下し、
流れる電流が更に増加することで、Lが急激に低下します。
一次インダクタンスLp
算出したIpを使い、一次巻線のインダクタンスLpを求めます。

Vin:入力電圧の最小値 [V]
ton:スイッチングON時間 [s]
Ip:一次側ピーク電流 [A]
k:ピーク電流Ipに対する直流成分の割合(k<1)
<計算例>
本例のLpを求めると、
Lp=Vin・ton/Ip
=108 × 10 × 10-6/1.3
≒830 × 10-6 [H]=830 [uH]
<参考:(3),(4)式になる理由>
インダクタンスの公式より
Vin=Lp・di/dt
変形すると(3)式になります。
Lp=Vin・dt/di=Vin・ton/Ip
連続モードの場合は、
Lp=Vin・dt/di=Vin・ton/[(1-k)Ip]
=Vin・ton/[(1-k)Ip]
となり、(4)式になります。
一次側巻き数Np
算出したIp、Lpを使い、一次巻線の巻き数Npを求めます。

Lp:一次巻線のインダクタンス [H]
Ip:一次側ピーク電流 [A]
Ae:コアの実効断面積 [m2]
ΔB:磁束密度の変化量 [T] =( Bs(飽和磁束密度) ー Br(残留磁束密度) ) × 0.6~0.8
コア材の選定で説明した磁束密度の変化量ΔBになります。
ここで0.6~0.8を掛けているのは、過負荷時に電流が多く流れても、
Bが飽和しないようにするためマージンをとっています。
<計算例>
本例のNpを求めると、FEER-28LはデータシートよりAe=81.4mm2、
ΔBはコア材PC95について、温度100℃の値(Bs=410mT、Br=60mT)から計算しました。
ΔB= (410ー60) × 0.6=210 [mT]
Np=Lp・Ip/(Ae・ΔB)
=830 × 10-6 × 1.3/(81.4 × 10-6 × 0.21)
≒64 [ターン]
<参考:(5)式になる理由>
磁束密度の公式より
磁束Φ=B・Ae
B=u・H、H=Np・Ip/ℓなので、(ℓ:コアの磁路長)
Φ=B・Ae=u・H・Ae
=u・Np・Ip・Ae/ℓ
Lp=N・pΦ/Ipなので
Lp=Np・(u・Np・Ip・Ae/ℓ)/Ip
=Np2・u・Ae/ℓ
変形すると
u/ℓ=Lp/(Np2・Ae)
この式をB=u・Hに代入すると、
B=u・H=Np・Ip・u/ℓ
=Np・Ip・Lp/(Np2・Ae)
=Lp・Ip/(Np・Ae)
変形すると(5)式になります。
Np=Lp・Ip/(Ae・B)
ギャップ長ℓg
フライバック電源は一次側FETがON時にトランスのコイルにエネルギーを蓄えておき、
OFFになったら、そのエネルギーを二次側に供給することで電力を出力します。
トランスにエネルギーを蓄えるにはギャップが必要です。

ギャップによりエネルギーを蓄えることができる仕組みは、
コンデンサが電極間(つまりギャップ)にエネルギーを蓄積できることと似ています。
コンデンサのギャップで電流の流れをせき止めることで電気エネルギーを貯めるのと同様に、
コアのギャップにより、磁束の流れをせき止めることで磁気エネルギーを貯めているのです。
また、ギャップを設けると、直流重畳特性が改善し、電流を多く流せるようになります。
直流重畳特性とは、
巻線に流す直流電流を増やしていくと磁気飽和により、
インダクタンスが低下する現象のことです。
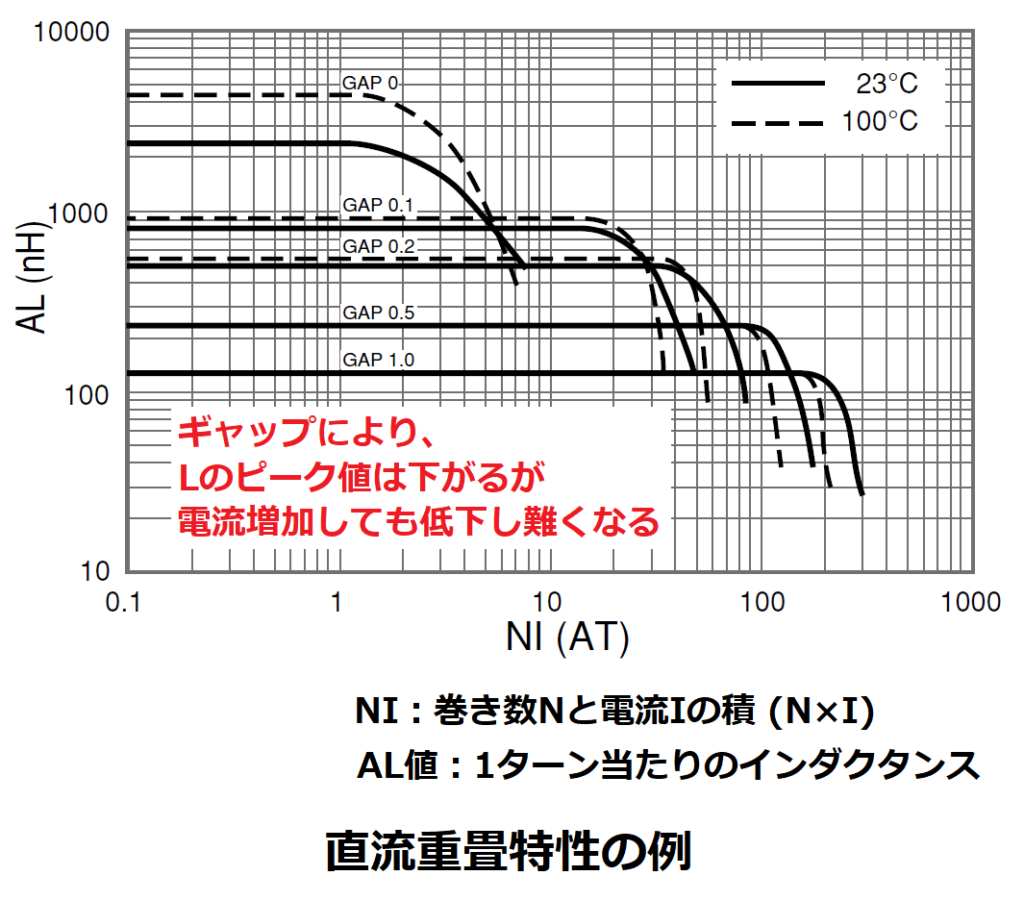
直流重畳特性のグラフを見ると、
ギャップを設けることで、インダクタンスLを低下させずに
流すことができる電流が増えていることがわかります。
(詳しくは後で説明します)
ギャップ長ℓgを求める式は以下になります。

Np:一次巻線の巻き数 [T]
μ0:真空の透磁率 =4π×10-10 [H/mm](単位がH/mでないことに注意)
Ae:コアの実効断面積 [mm2]
Lp:一次巻線のインダクタンス [H]
<計算例>
本例のℓgを求めると、
ℓg=Np2・μ0・Ae/Lp
=642 × 4π × 10-10 × 81.4/(830 × 10-6)
≒0.5 [mm]
ℓgを求める方法として、上記の式以外にも
LpとNpからAL値を計算し、グラフからℓgを求めることもできます。
AL=Lp/Np2
=830 × 103[nH]/642
≒ 203 [nH/N2]
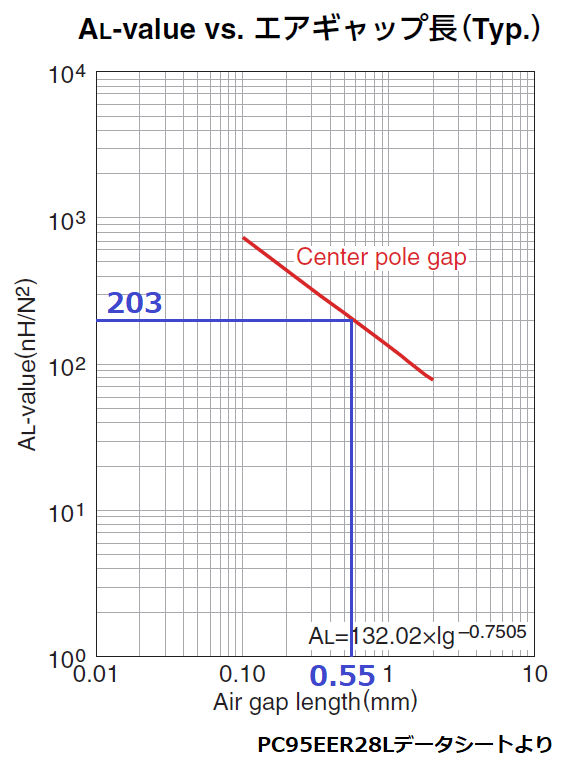
データシートのALーℓgグラフより、ℓg=0.55mmとなり、
先程の計算値とほぼ一致します。
<参考:(6)式になる理由>
コアを磁気回路で表した場合、
磁束の流れ難さを表す磁気抵抗Rは以下の式になります。
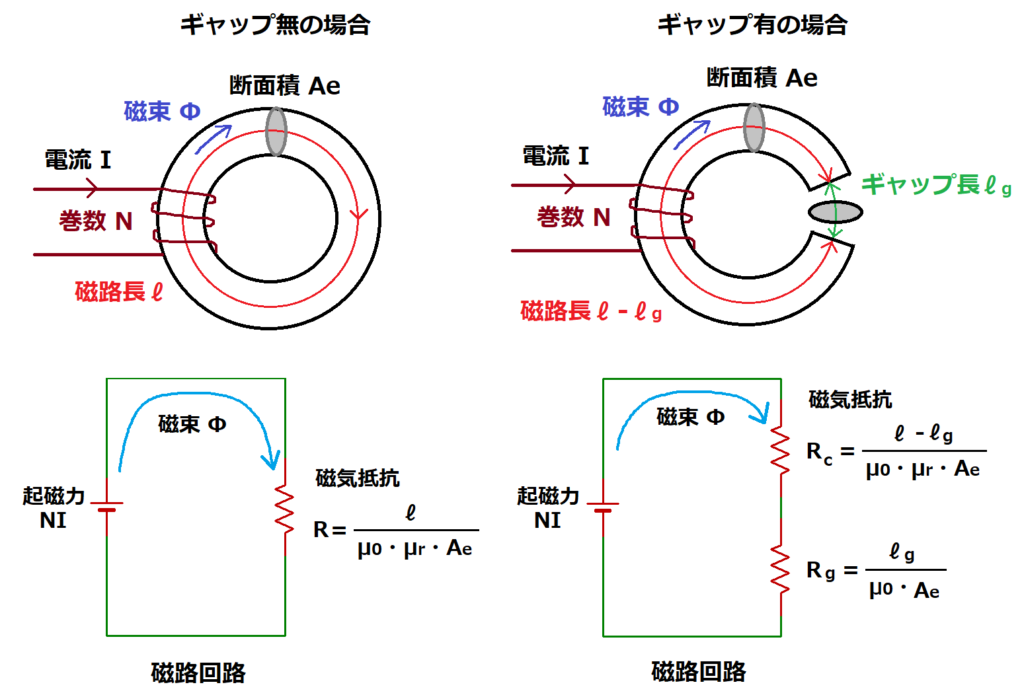
磁気抵抗R=ℓ/(u0・ur・Ae)
ℓ:コアの磁路長
ur:コアの比透磁率
Ae:コアの実効断面積
コアにギャップℓgを設けた場合の磁気抵抗Rは
コア部分をRc、ギャップ部分をRgとすると以下になります。
R=Rc+Rg
=(ℓーℓg)/(u0・ur・Ae)+ℓg/(u0・Ae)
=1/(u0・Ae)×((ℓーℓg)/ur+ℓg)
ギャップ長ℓgはコアの磁路長ℓに比べて十分短いので、ℓーℓg≒ℓとすると、
R=1/(u0・Ae)×(ℓ/ur+ℓg)
比透磁率urはトランス用フェライトで1500~3000となっていることから、
ℓgに比べ、ℓ/urは無視できる程小さくなるので、
R≒ℓg/(u0・Ae)
ここで、単位巻線あたりのインダクタンス値を示すAL値を使用します。
AL=Lp/Np2
このAL値と磁気抵抗Rの関係はAL=1/Rとなっているので、
AL=1/R=(u0・Ae)/ℓg
式を変形すると
ℓg=(u0・Ae)/AL
これにAL値の公式 AL=Lp/Np2を代入すると(6)式になります。
ℓg=Np2・μ0・Ae/Lp
<参考:ギャップにより、磁気飽和が発生し難くくなる理由>
先ほどの磁気抵抗の説明で、
ギャップが無い場合のコアの磁気抵抗Rは
R=ℓ/(u0・ur・Ae)
ギャップを設けた場合は
R=ℓg/(u0・Ae)
となることを説明しました。
これは、ギャップを設けることで、コア固有の値である
比透磁率μrや磁路長ℓの影響を受けなくなることを意味します。
それはつまり、コアの透磁率が(μr・μ0)からu0に減少したことになります。
(厳密にはギャップ間は真空ではないので、μrはわずかながら存在します)
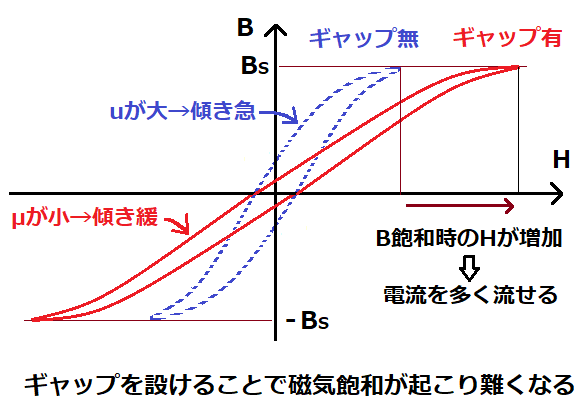
また、B=μHより、透磁率μはB-H曲線の傾きに相当し、
μが小さくなると傾きが緩やかになるため、
H(つまり電流)を増やしても、Bがすぐに飽和しなくなります。
二次側巻き数Ns
算出したNpを使い、二次巻線の巻き数Nsを求めます。
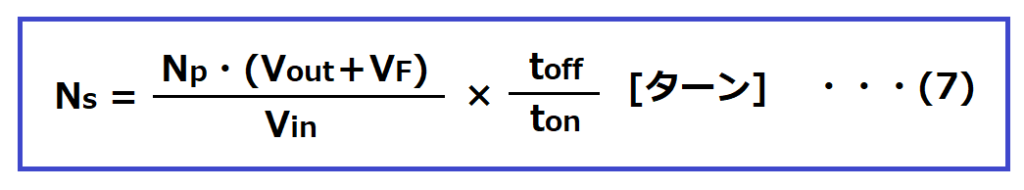
Np:一次巻線の巻き数 [ターン]
Vout:出力電圧 [V]
VF:二次側回路の整流ダイオードの順方向電圧 [V]
Vin:入力電圧の最小値 [V]
ton:スイッチングON時間 [s]
toff:スイッチングOFF時間 [s] =周期Tーton
多出力にする場合は、メインとなる出力電圧の巻き数を決め、
メイン出力電圧/巻き数=二次側1巻きあたりの電圧
より、他の出力の巻き数を設定します。
例えば、12Vと5Vの2つの出力を持たせる場合、
12V出力の巻き数が8ターンとすると、1ターンあたり1.5Vなので、
5V出力の巻き数は5/1.5≒3.33=4ターンになります。
<計算例>
本例のNsを求めると、DUTYを0.5とした場合、toff/ton=1になるので、
使用する整流ダイオードのVFが0.7Vの場合、
Ns=Np・(Vout+VF)/Vin × toff/ton
=64 × (12 + 0.7)/108 × 1
=7.52 ≒8 [ターン]
<参考:(7)式になる理由>
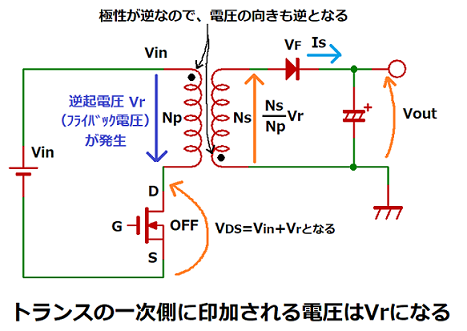
フライバック電源の場合、トランスの一次側電圧はVinではありません。
一次側電圧は、スイッチOFF時にトランスの一次側コイルで発生するフライバック電圧Vrになります。
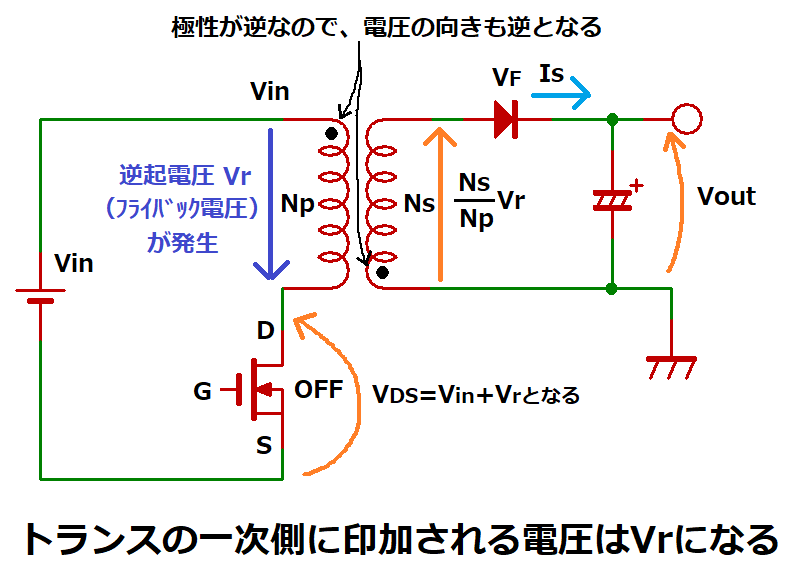
フライバック電圧とは、コイルに流れている電流を遮断した時に発生する逆起電圧の事です。
この逆起電圧が発生する仕組みについて説明します。
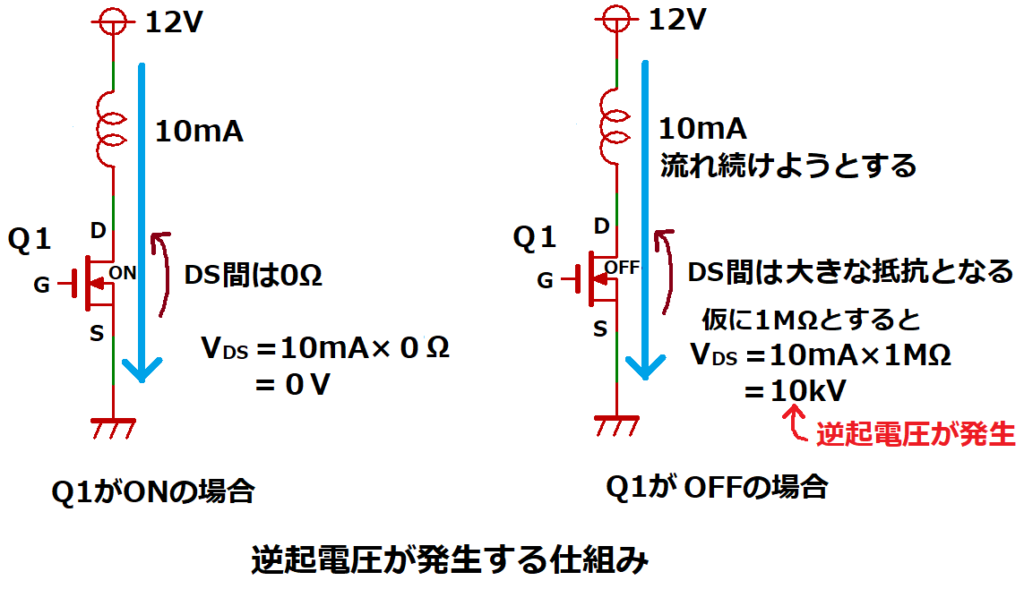
Q1がON時にコイルに10mA流れていたとします。
Q1がOFFすると回路が遮断されますが、
これはドレイン・ソース(DS)間に非常に大きな抵抗があると考えることができます。
(ここでは、仮に1MΩとします)
コイルは流れる電流を維持しようとする働きをします。
つまり、抵抗1MΩに10mA流れる事になるので、ドレイン・ソース間電圧VDSは
VDS=R×I=1MΩ×10mA=10kVと非常に高い電圧になります。これが逆起電圧です。
(実際には、ここまで高電圧にはなりません)
これをフライバック電源に置き換えて考えると、
図のようにトランス一次側入力の上側(極性マークのある側)の電圧はVinです。
FETがOFF時に一次側コイルに逆起電圧Vrが発生することにより、
下側(極性マークの無い側)の方がVrだけ電圧が高くなります。
トランスの極性マークを見ると、一次側と二次側の位置が上下逆になっています。
このため、トランスの極性マークの無い下側の一次側電圧が高くなると、
二次側電圧もマークの無い上側の電圧が高くなるので、整流ダイオードを経由して
電流Isが出力されます。
この逆起電圧であるフライバック電圧Vrと二次側電圧(Vout+VF)の関係は以下となります。
(Vout + VF)=Vr × Ns/Np
また、ON時に一次側に蓄えられたエネルギーが、OFF時に二次側に全て伝わるとした場合、
以下の式が成り立ちます。
Vin × Ip × ton=(Vout + VF) × Is × toff
この式に先程の式と、二次側電流Is=Ip× Np/Nsを代入すると、
Vin × Ip × ton=Vr × Ns/Np × (Ip × Np/Ns) × toff
Vin × ton=Vr × toff
Vr=Vin × ton/toff
となります。
Np/Ns=Vr/(Vout + VF)に、このVrの式を代入すると(7)式になります。
Ns=Np・(Vout + VF)/Vin × toff/ton
線径を求める
巻線の単位面積あたりの許容電流を電流密度(電流容量)と呼びます。
トランスに使用されるエナメル線の電流密度は3~5 [Arms/mm2]程度です。
ここでは、この電流密度を目安にして、巻線に流れる電流の実効値から必要な線径を算出します。
<一次巻線の線径>
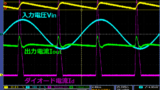
フライバック電源の一次側電流は三角波がton時に流れるので、実効値Ip(rms)は
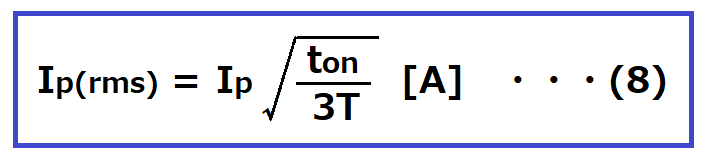
Ip:一次側ピーク電流 [A]
ton:スイッチングON時間 [s]
T:スイッチング周期 [s]
電線に流れる電流の実効値がIrmsの場合、必要な線径Φdは以下の式で求まります。

Irms:電流(実効値)[A]
δ:電流密度(3~5 [Arms/mm2])
<計算例>
本例のIp(rms)を求めると
Ip(rms)=Ip√(ton/3T)
=1.3 ×√[(10 × 10-6)/(3 × 20 × 10-6)]
≒0.53 [A]
一次側巻き線の線径Φdpについては、電流密度を3 [Arms/mm2]とした場合、
Φdp=2 ×√(Irms/(π × δ))
=2 ×√(0.53/(π × 3))
≒0.47 [mm]
<二次巻線の線径>
二次側電流Isも実効電流値を求めますが、
一次側と違い、平均電流である出力電流Ioutから求めます。
また、toffの時に電流が流れるので、以下の式となります。

Iout:出力電流 [A]
toff:スイッチングOFF時間 [s]
T:スイッチング周期 [s]
<計算例>
本例のIs(rms)を求めると
Is(rms)=2×Iout√(T/3toff)
=2 × 2.5 × √(20 × 10-6/3 × 10 × 10-6)
≒4 .08A
二次側は一次側と比べ、巻き数が少ないので巻線長が短くなります。
また、ボビンに巻く時、基本的には一次側巻線の外側に巻くため、
温度が低くなることから、電流密度は一次側よりも大きくできます。
二次側巻き線の線径Φdsは、一次側と同様に(9)式で求めます。
電流密度を5 [Arms/mm2]とすると、
Φds=2 × √(Irms/(π × δ))
=2 × √(4.08/(π × 5))
≒1.0[mm]
線径がΦ0.5以上だと、硬くて巻き難くなります。
このため、複数本に分け、1本あたりの電流値を減らすことで、線径を細くできますが、
3本を超えると巻き難いので、リッツ線を使用すると良いです。

リッツ線は、細い素線を撚り合わせて1本にした電線で、
表皮効果の影響を抑えることができることから、
電流密度も6~8 [Arms/mm2]程度まで大きくできます。
ここでは、Φ0.12×45本のリッツ線を使用します。
断面積は0.062 × π × 45≒0.51mm2となり、
電流密度を8 [Arms/mm2]とすると、
流せる電流は0.51 × 8≒4.08Aとなるので、本例で使用できます。
ここで使用した電流密度は、あくまで目安なので、
実際にはトランスを試作し、動作時の巻線温度を測定し、
エナメル線の耐熱温度である120℃以下になるようにします。
この時、測定時の周囲温度が25℃で、電源仕様の周囲温度上限が60℃としたら、
その温度差35℃を巻線温度測定値に加えても120℃以下にしなくてはなりません。
巻線の温度は絶縁テープを介して熱電対で測定しますが、
それは、外側に巻かれている二次巻線の温度であり、
内側にある一次巻線の方が熱くなることを考慮し、マージンを取る必要があります。
また、コアのサイズ・形状によっては、巻線に熱電対をつけにくい為、
線径を変えて都度比較する際は、コアの温度を測定し、
その温度に10℃プラスした値を巻線温度の目安にできます。
<参考:(8)式になる理由>
三角波の実効値の公式より、ピーク電流をIpとすると、
Ip(rms)=Ip/√3
これが周期Tのうちtonだけ出力した場合、
√(ton/T)倍されるので、(8)式になります。
Irms=Ip × √(ton/3T)
<参考:(9)式になる理由>
電線の断面積をSとすると、電流密度δは以下の式になります。
δ=Irms/S
S=π × (Φ/2)2なので、代入すると、
δ=Irms/(π × Φd2)/4
変形すると(9)式になります。
Φd=2 × √((Irms/(π × δ))
<参考:(10)式になる理由>
三角波の平均電流Iaveは、ピーク電流Ipeakの場合、以下の式になります。
Iave=1/2・Ipeak・(toff/T)
三角波の実効値の公式Irms=Ipeak/√3 を組み合わせると、
Irms=2Iave/(toff/T)/√3
これが周期Tのうちtoffだけ出力した場合、
√(toff/T)倍されるので、(10)式になります。
Irms=2Iave/(toff/T)/√3 ×√(toff/3T)
=2Iave・√(T/3toff)
巻き厚を確認する
求めた巻き数と線径で、巻線がコアに巻けるか確認します。

コアのカタログには、巻線断面積Awが記載されており、
ここが、巻き線を通す部分になりますが、
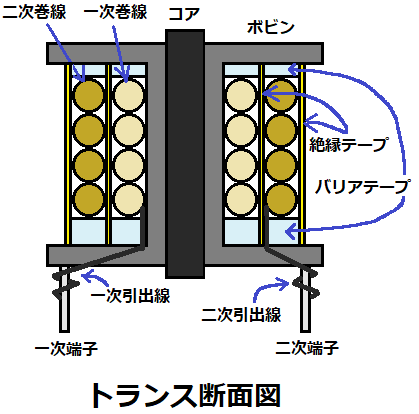
実際には、巻き線はボビンに巻くため、これよりも面積は小さくなります。
また、巻く際に絶縁テープやバリアテープを貼ったり、
巻く時に緩みが発生するため、Awに対し巻線の占める割合が50%程度に収まるようにします。
一方、巻き線の断面形状は円ですが、
実際の専有面積は図のように直径×直径の正方形になります。
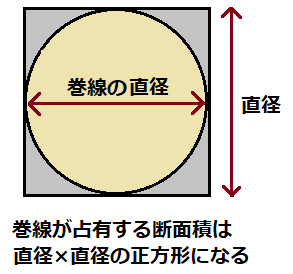
以上のことから、巻線が占める面積は以下の式を満足する必要があります。
Acw × 0.5 > 一次側線径Φdp2 × 一次巻数Np+二次側線径Φds2 × 二次巻数Ns
これ以外に、別出力の巻線がある場合はその分も加えます。
<計算例>
FEER-28Lの巻線断面積Acwは、データシートより148mm2なので、
巻線が占めることができる面積を50%とすると、
148 × 0.5=74mm2
一次巻線の占める面積は、Φdp=0.47mm、Np=64より、
0.472×64=14.2mm2
二次巻線の占める面積はΦ0.12×45のリッツ線をNs=8ターンするので、
0.122 × 45 × 8 ≒ 5.2mm2
巻線の占める面積の合計は
14.2+5.2=19.4mm2
となり、巻くことが可能な面積74mm2よりも十分小さいため、
ボビンに巻き線を巻くことが可能です。
★フライバック・コンバータの動作原理について説明しています。
以下の記事で、試作時で役立つ工具類を紹介しています。