この記事でわかること
・負電圧回路や倍電圧回路の動作原理
・チャージポンプICの使い方
・リップル電圧、出力インピーダンスの求め方
電源電圧を上げたい、あるいは負電圧の電源を作りたい場合、
チャージポンプ回路を利用することで、必要な電源電圧を得ることができます。
この回路の長所は、
・チャージポンプICを使えば、負電圧ならコンデンサ2個、
倍電圧なら更にダイオード2個を追加するだけで構成可能
・コイルを使わないので放射ノイズが少ない
・軽負荷でも90%以上の高効率が可能
短所は、
・コンデンサに充電させたエネルギーを利用するため、大電流は出力できない
・コンデンサの充放電に伴う出力電圧の振幅(リップル電圧)が大きい
・出力電流が増えると出力電圧が低下する(出力インピーダンスが大きい)
このように一長一短ありますが、
場所を取らない小電力電源として、RS-232C通信用IC(MAX232など)では
チャージポンプ回路を内蔵しており、5V電源から通信に必要な±12Vを生成しています。
本記事では、チャージポンプ回路の動作原理と、
チャージポンプICのロングセラー品として有名なICL7660の使い方について解説します。
チャージポンプ回路の動作原理
1.負電圧回路
入力電圧Vinを負電圧-Vinに変換する回路です。
OSCにはパルス信号が入力されます。
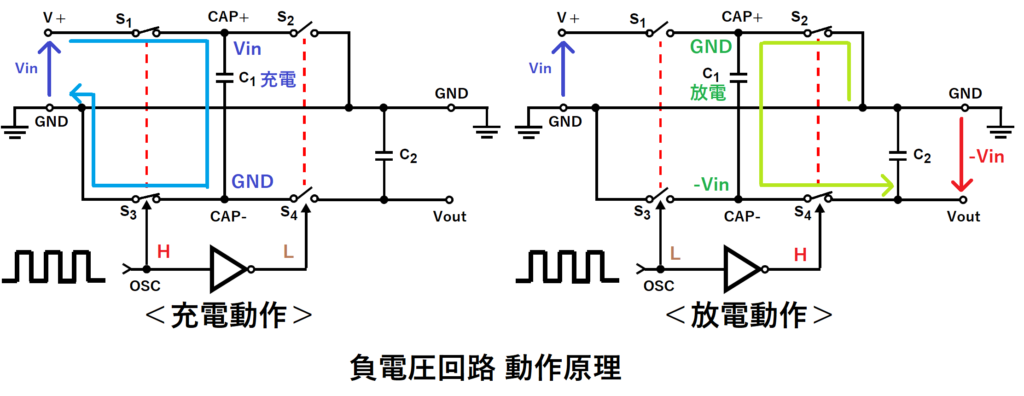
OSCがHの時はS1、S3がオン、S2、S4がオフするので、
C1は電圧Vinに充電されます。
この時、CAP+が電圧Vin、CAP-がGNDになります。
次にOSCがLの時はS1、S3がオフ、S2、S4がオンするので、
C1が放電し、C2が充電されます。
この時、先程まで電圧VinだったCAP+がGNDになるので、
CAP-はその分マイナスにシフトするので電圧が-Vinになります。
この結果、C2は電圧-Vinに充電されるので、
出力Voutの電圧は、入力電圧Vinを反転した-Vinとなります。
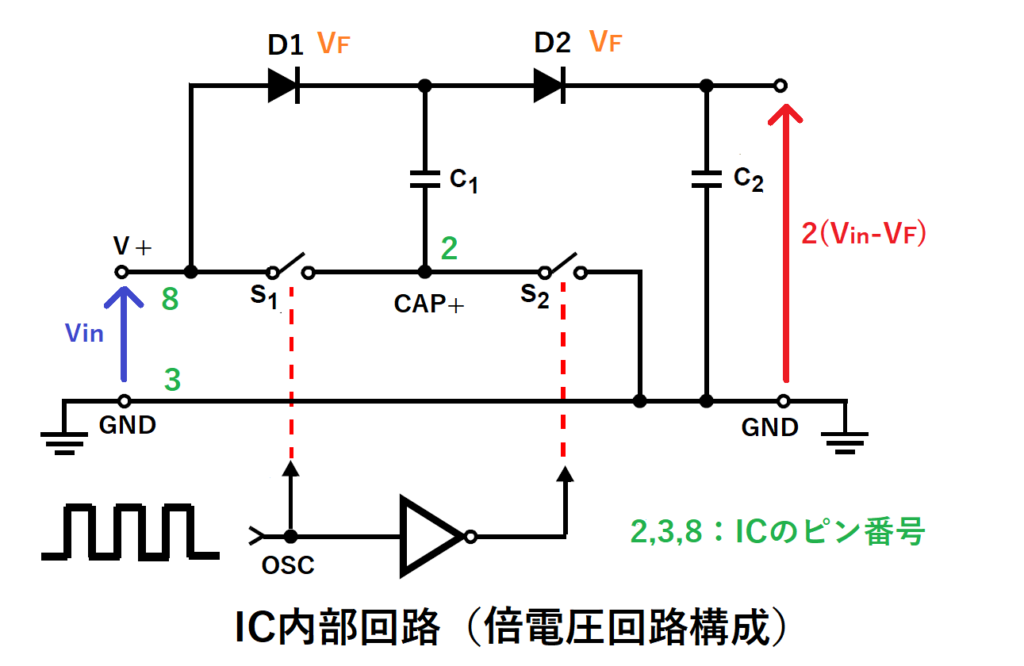
2.倍電圧回路
入力電圧Vinを約2倍の電圧2(VinーVF)に変換する回路です。
ここでVFはダイオードD1、D2の順方向電圧です。
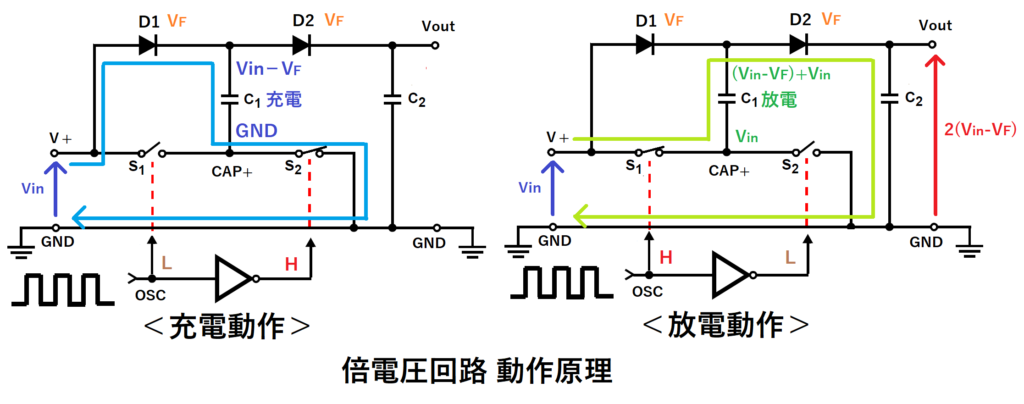
OSCがLの時はS1がオフ、S2がオンするので、C1が充電されます。
この時、C1の電圧はD1を経由するので、
ダイオードの順方向電圧VF分だけ低下するので
C1電圧=VinーVF
となります。
次にOSCがHの時はS1がオン、S2がオフすると、
先程までGNDだったCAP+が電圧Vinになるので、
C1電圧はVin分かさ上げされ、
C1電圧=(VinーVF)+Vin
となります。
この時、D1があるので、電圧の低いV+側には電流は流れません。
C2の電圧はD2を経由するので、
ダイオードの順方向電圧VF分だけ低下するので
C2電圧=C1電圧ーVF
=2(Vin-VF)
となります。
その後、再びOSCがLとなると、C1電圧はVinーVFに低下しますが、
D2によって、C2からC1側に電流は流れないので、
C2電圧(出力Vout)は2(Vin-VF)のままです。
D1,D2を順方向電圧VFの低いショットキーダイオードにすれば、
出力Voutは入力電圧Vinの約2倍の電圧となります。
このように、チャージポンプ回路は、
コンデンサとスイッチを組み合わせて、負電圧や倍電圧を得ているので、
スイッチドキャパシタとも呼ばれています。
スイッチドキャパシタについて
スイッチドキャパシタはコンデンサを抵抗のように扱うことができます。
この動作が分かると、
この後出てくる出力インピーダンスの存在が理解できます。

スイッチが左側の時、コンデンサCは電圧V1に充電されます。
Cに充電された電荷はQ1=CV1になります。
次に、スイッチが右側に切り替わった時、Cは放電されます。
出力電圧がV2になった時、Cの残留電荷はQ2=CV2です。
Cが失った電荷量(つまり負荷RLに流れた電荷量)は
ΔQ = Q1 – Q2 = C(V1 – V2)
になります。
このスイッチ動作が1秒間にf回(周波数f)行われた場合、
1秒間に流れた電荷量(つまり電流I)は次のようになります。
l =f × ΔQ = f × C(V1 – V2)
式を変形すると
I=(V1ーV2)/(1/f×C)
=(V1ーV2)/REQUIV
で表現できます。
つまり、コンデンサCが抵抗REQUIVとして働くことを意味します。
REQUIV=1/(f×C)
等価回路に置き換えると以下のようになります。
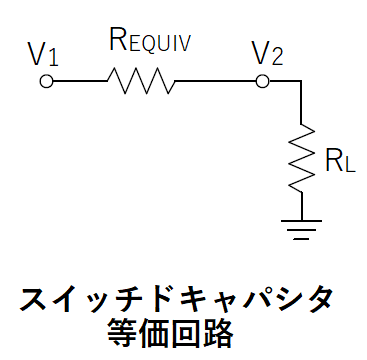
これがチャージポンプ回路における出力インピーダンスとなり、
電流Iを流した時、出力電圧はI×REQUIV分電圧降下します。
※実際には、コンデンサ内の抵抗成分(等価直列抵抗ESR)による電圧降下も存在します。
これについては後で説明します。
このことから、
チャージポンプ回路はどれくらいの電流が流せるか?を考えた場合、
この出力インピーダンスで決まってしまいます。
この後、解説する負電圧回路の出力インピーダンスは68Ωありますが、
この回路で50mA流したら、出力電圧-5Vを出力するところが、
50mA×68Ω=3.4Vも電圧降下する(出力電圧が-1.6Vになる)ため、
使い物にならないことがわかります。
チャージポンプICの使い方
インターシル(現ルネサス)製ICL7660や、
リニアテクノロジ(現アナログデバイセズ)製LTC1044は、
昔からある有名なチャージポンプICで、他社からセカンドソース品も出ています。
TC7660、TC1044 マイクロチップ
NJU7660 新日本無線(現 日清紡マイクロデバイス)
MAX1044 マキシム(現 アナログデバイセズ)

1ピンはメーカーによって、
未使用(NC)又はBOOST(ブースト)ピンとなっています。
BOOSTピンの場合、これを電源ピン(V+)と接続すると
発振器周波数が数倍(メーカーによって異なる)に増加します。
これによって、スイッチング周波数を可聴域(20kHz以上)より高くしたり、
外付けコンデンサの容量を小さくすることもできます。
また、リップル電圧や、出力インピーダンスも低減できますが、
スイッチング損失が増えるので効率は低下します。
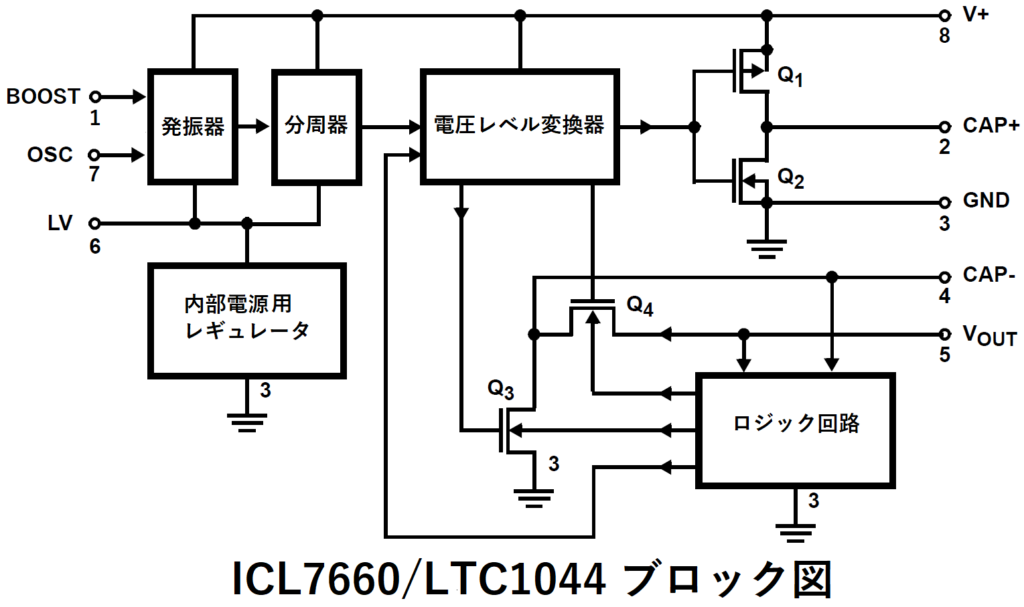
発振器と分周器により、発振器周波数の1/2の周波数で
50%デューティのオン・オフ用パルスを生成し、
電圧レベル変換器で4つのスイッチ(FET Q1~Q4)を切替えます。
(※つまり、スイッチング周波数は発振器周波数の1/2です)
ロジック回路は電圧の極性に応じて、
Q3、Q4のソース(S)とドレイン(D)を切り替えています。
これを行うことで、
ドレインよりソース電圧が高くならないようにします。
(ソースの方が高くなると、ゲートがオフしていても、
FETのボディダイオードにより電流が流れてオン状態になる為)
内部電源用レギュレータは内部回路用の低電圧電源を供給します。
この内部電源は入力電源V+が低い時(3.5V以下)は使用しない為、
その際は、LV端子をGNDに接続します。
<注意点>
本記事で解説するチャージポンプICの使い方は一般的な内容です。
各メーカーで仕様が異なっており、
ここで紹介する方法が適切で無い場合がある為、
使用の際は、デバイスのデータシートを必ず確認して下さい。
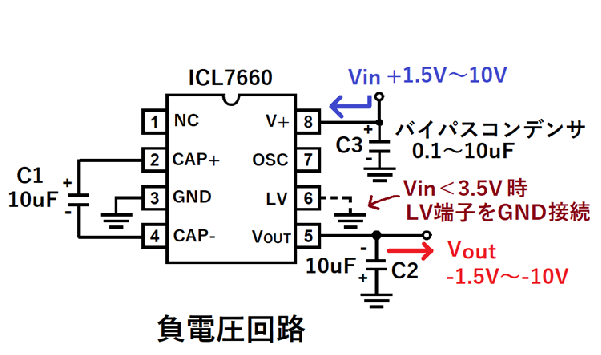
負電圧回路
図のようにコンデンサC1、C2を接続することで、
動作原理で説明した負電圧回路になります。

入力電圧Vinに対して、出力電圧Vout=-Vinが出力されます。
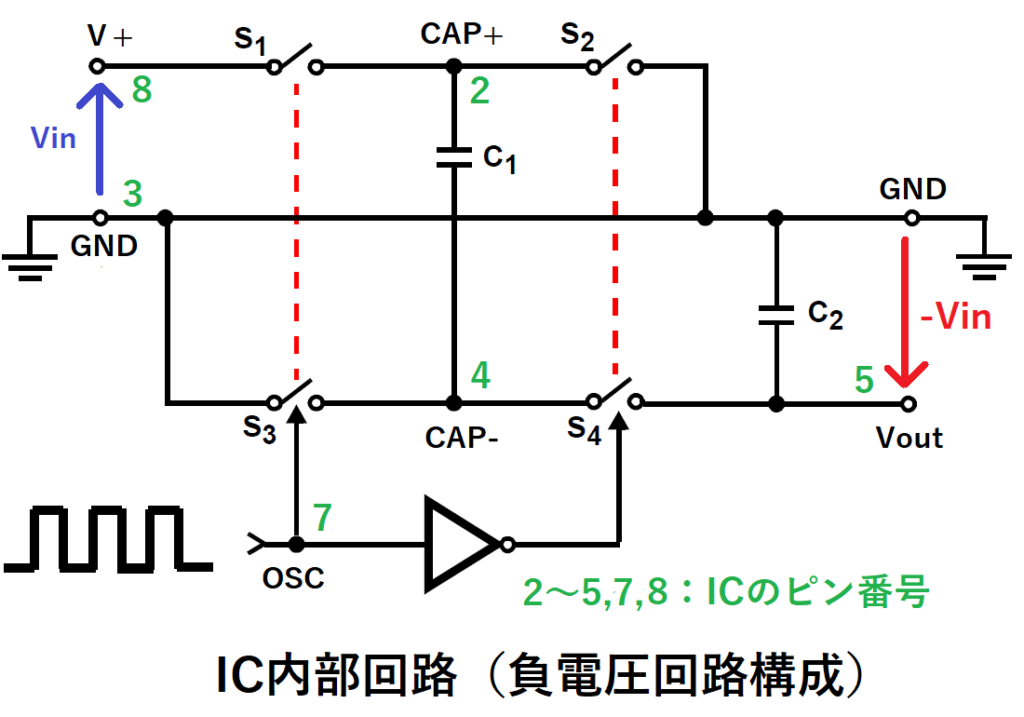
入力電圧が3.5V以下の場合は、内部低電圧電源を無効にするため、
LV端子をGNDに接続します。
C3はICに一般的に使用する電源安定用のバイパスコンデンサ(パスコン)です。
通常は0.1uFで良いと考えますが、各社データシートの適用例を見ると
0.1~10uFと幅広いです。
出力インピーダンス
一般的なスイッチング電源と比べ、
チャージポンプ回路の出力インピーダンスは大きく、
出力電圧は出力電流の大きさに比例して低下します。

入力電圧Vinに対して、出力電流Iが流れる時、
出力電圧VoutはRo×I分低下します。
Vout=-Vin+Ro×I
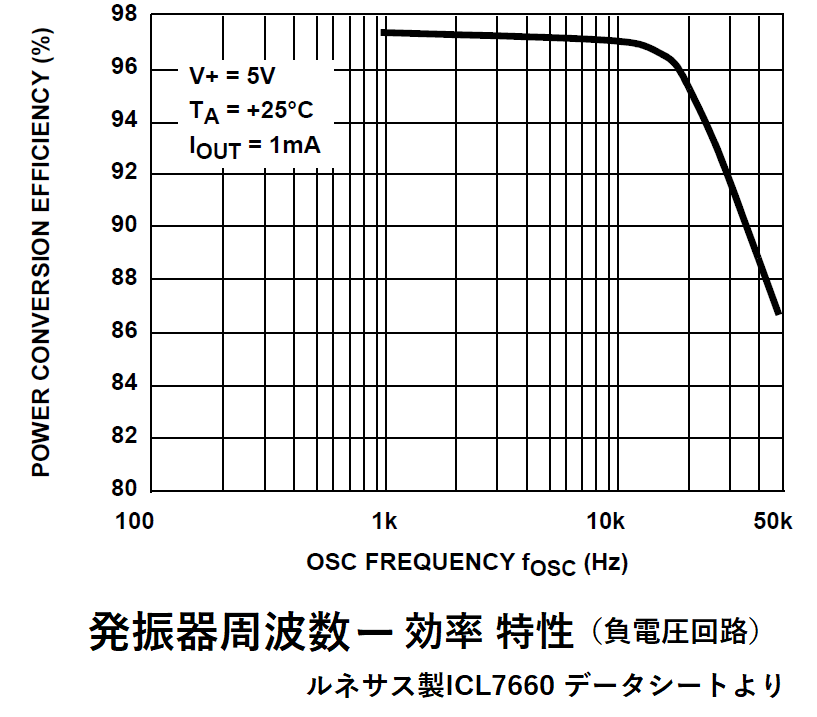
ICL7660のデータシートより、
出力インピーダンスRoは以下の近似式で定義されています。

RSW1~RSW4 :内部スイッチ(FET Q1~Q4)のオン抵抗
RSW:4つの内部スイッチの合計値
データシートによると、
この値は電源電圧と温度で変化し、
通常は5V 25℃で23Ωであると記されてます。
fOSC:発振器周波数
この値は、後で説明する周波数調整をしない限り10kHzですが、
入力電圧Vinによって変動します。
fPUNP:スイッチング周波数 発振器周波数fOSCを1/2に分周したものです。
ESRC1、ESRC2:C1、C2の等価直列抵抗(ESR)
ESRはコンデンサの抵抗成分です。
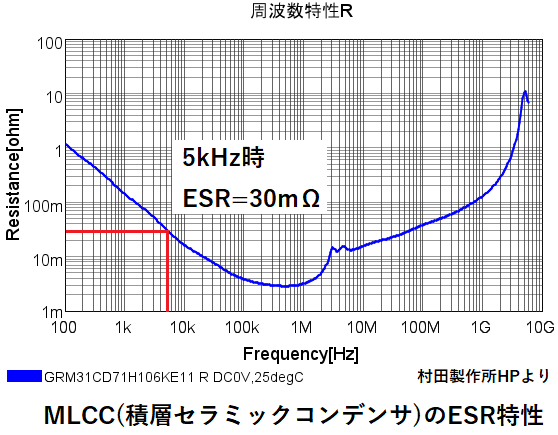
できるだけ小さい方が良いため、MLCC(積層セラミックコンデンサ)を使用します。
ESRの値は村田製作所やTDK製については、HP上で公開されています。
Cの容量ですが、高容量のMLCCでは、DCバイアス特性を考慮する必要があります。
DC バイアス特性とは印加されるDC 電圧によって容量が変化する特性のことで、
高誘電率型のMLCCの場合、一般的に電圧が上昇すると容量が減少します。
温度補償型ならDC電圧が高くなっても容量が殆ど変化しませんが、
チャージポンプで使用する10uFの高容量ではありません。
この減少の度合いは、耐圧が低く、チップサイズが小さい程顕著になります。
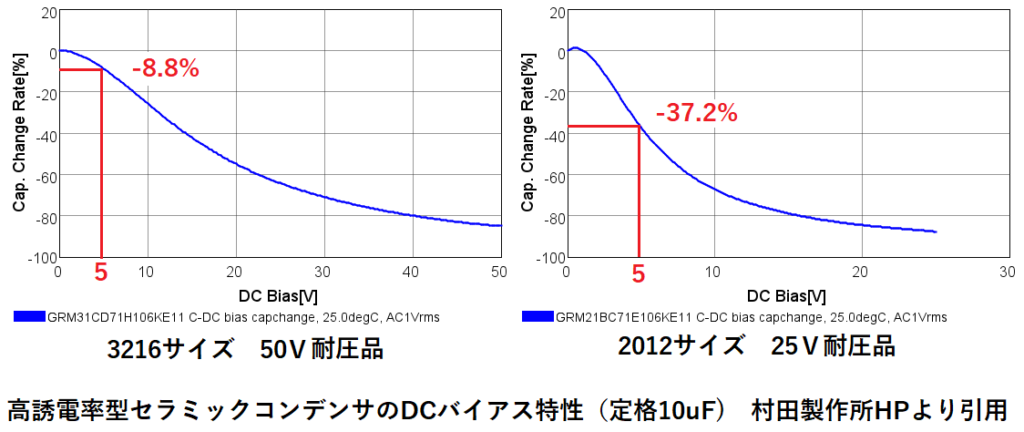
定格容量10uFの場合、DC5V印加時の容量変化率を見ると、
3126サイズの50V耐圧品では-8.8%ですが、
2012サイズの25V耐圧品になると、-37.2%も低下します。
Cが小さくなると、Roが大きくなってしまうので、
できるだけ耐圧が高く、チップサイズの大きいものを選びます。
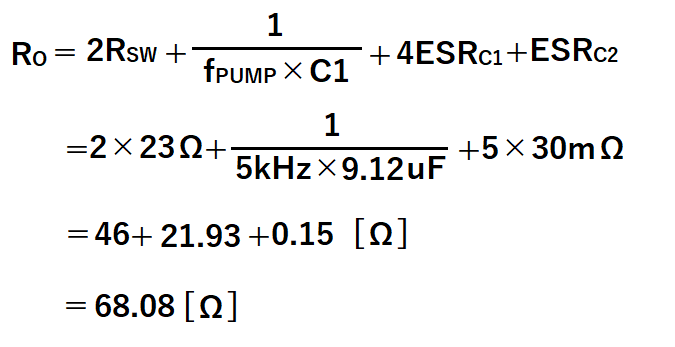
Vin=5V、fPUNP=5kHz、C1= C2 =10μFの場合のRoを計算してみます。
ESRは先程のグラフより、ESR=30mΩ
Cについては50V耐圧品を利用した場合、
DCバイアス特性より5V印加時は-8.8%減少するので、
C=10×(1ー0.088)=9.12uF
よって、出力インピーダンスRoは以下となります。
リップル電圧
リップル電圧は図のように、AとBの2つの電圧降下の合計値になります。
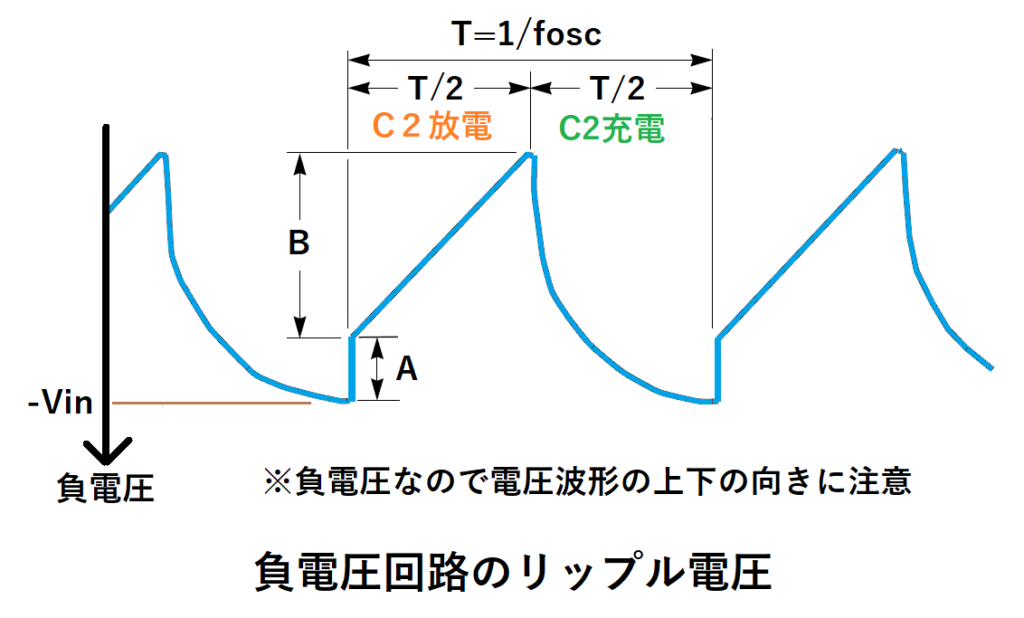
<A部分>
この電圧降下はC2が充電から放電に切り替わった瞬間に発生します。
(負電圧が減るので、電圧がAだけ上昇する形になります)
この時の電圧降下量Aは、出力電流Ioutの時、以下となります。
A=2(ESR×Iout)
この式になる理由ですが、
C2充電完了時、Vout=-Vinとなりますが、(※1)
C2の充電電圧はESRによって、ESR×Iout分電圧降下します。
※正確にはC1のESRによる電圧降下のため、Vout=-Vin+ESR×Ioutとなりますが、
出力電圧の変動幅には関係ないため、ここでは無視します。
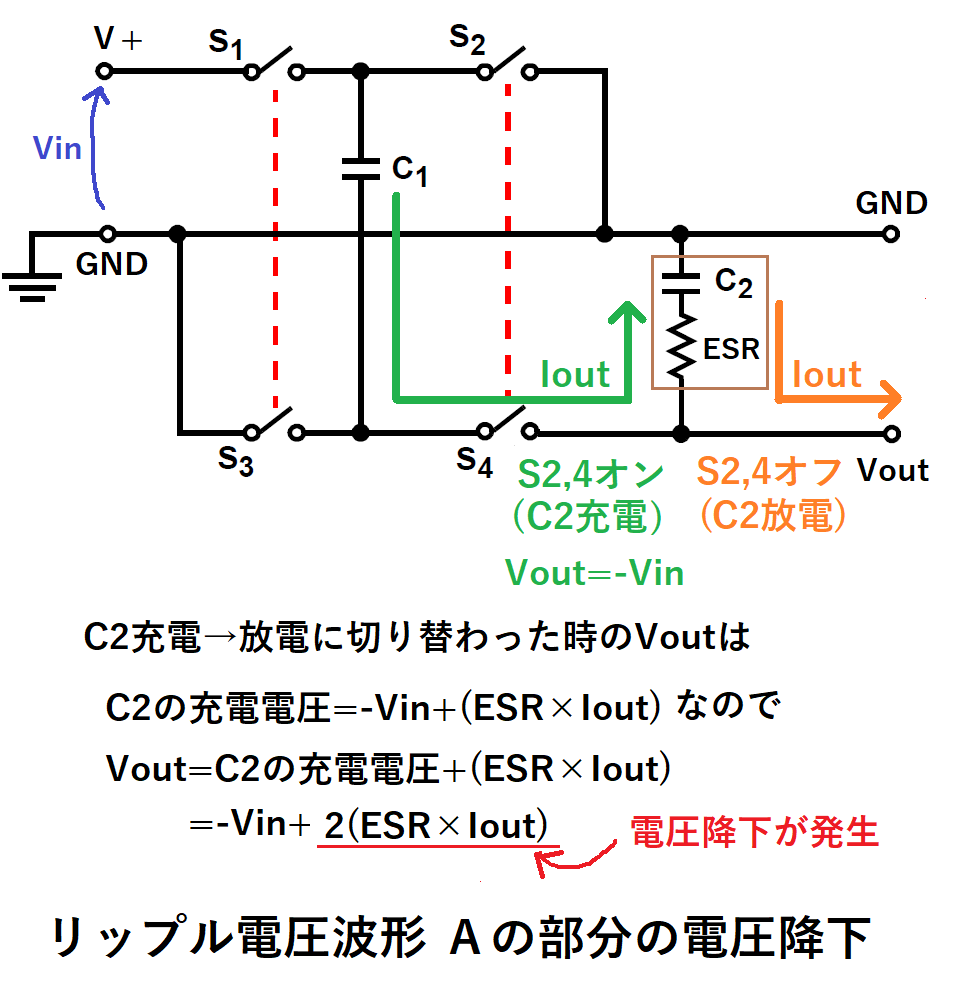
C2が放電開始時、VoutはC2の充電電圧から更にESR×Iout分電圧降下します。
従って、VoutはESR×Ioutの2倍電圧降下したことになります。
<B部分>
この電圧降下はC2放電時間中、出力電流Iout流れたことによるC2の電荷量の減少によるものです。
C2の放電時間tは、スイッチング周期T(=1/fpump)の半分なので、
t=1/(2fpump) となります。
減少した電荷量Qは以下になります。
Q=Iout×t=Iout/(2fpump)
この時の、電圧降下分ΔVは、Q=CVより、
ΔV=Q/C2 =Iout/(2fpump×C2)
これがそのままB=ΔVとなるので、
B=Iout/(2fpump×C2)
以上から、リップル電圧Vp=A+Bは以下となります。
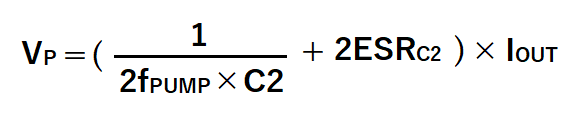
例として、
fPUMP=5kHz、ESR=30mΩ、C2=10uFの負電圧回路で、
出力電流1mAの場合で計算してみます。
Cは定格10uFですが、先程説明したDCバイアス特性により
C=9.12uFとなるので、
Vp=(1/(2×5kHz×9.12uF)+2×30mΩ)×1mA
=11mV
となります。
倍電圧回路
図のようにコンデンサC1、C2、ダイオードD1、D2を接続することで、
動作原理で説明した倍電圧回路になります。
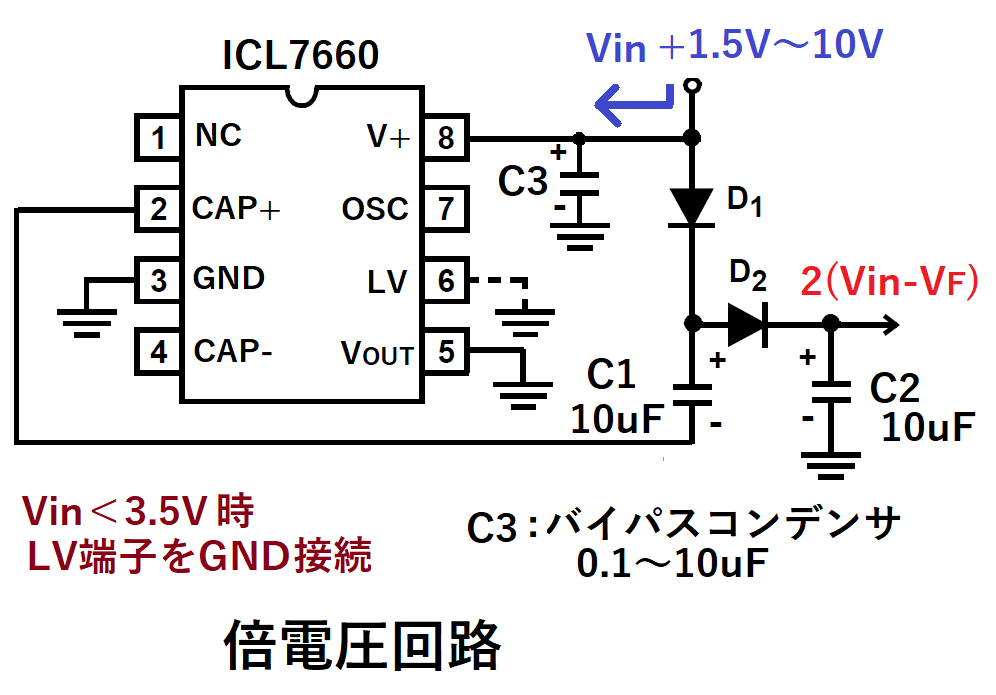
入力電圧Vinに対して、約2倍の電圧2(VinーVF)を出力できます。
順方向電圧VFを小さくするため、
D1、D2にはショットキーダイオードを使用します。
負電圧回路と同様、入力電圧が3.5V以下の場合は、
内部低電圧電源を無効にするため、LV端子をGNDに接続します。
発信周波数の調整
発振器周波数foscを上げると、出力インピーダンスRoや、リップル電圧Vpを小さくできます。
また、RoやVpを維持しまたま、コンデンサ容量を小さくすることもできます。
それ以外にも、スイッチングノイズを
可聴周波数帯域(20Hz~20kHz)外に退避させたい場合にも用いられます。
逆に、周波数を下げると、スイッチング損失やICの自己消費電流が減り、効率が向上します。
<周波数を上げる方法>
OSC端子に外部クロックを入力することで、
発振器周波数を外部クロック周波数にすることができます。
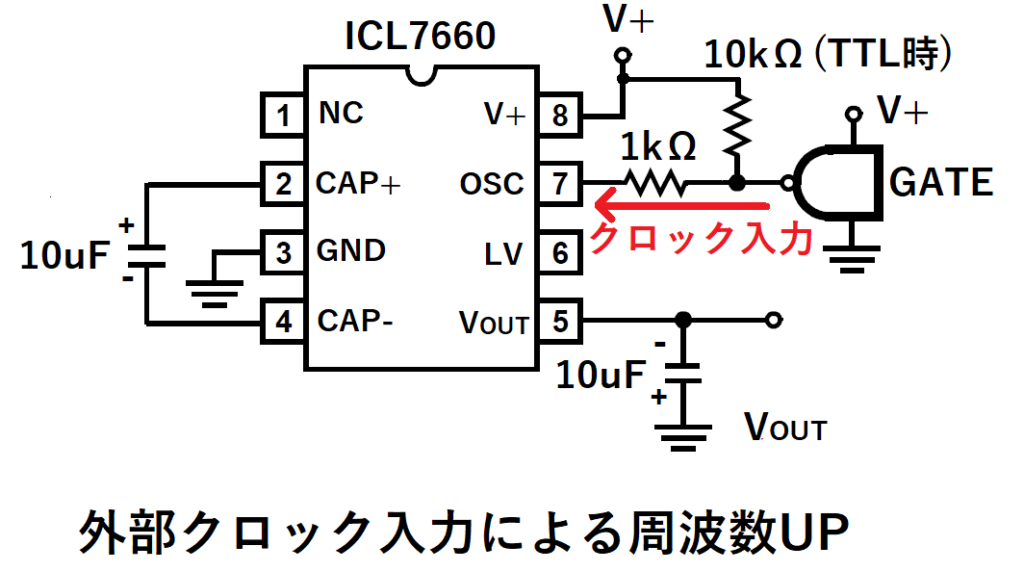
外部クロックを入力する際は、
ICのラッチアップ防止の為、1kΩの抵抗を接続して入力電流を制限します。
OSC端子の入力しきい値Vthは以下となります。
電源電圧V +が5V以上 Vth= V + - 2.5V
5V未満 Vth= V+ /2
このため、TTL ICだとHレベル出力が2.4Vで不足することから、10kΩでプルアップします。
この外部クロックですが、内部クロックと同様に分周されるので、
スイッチング周波数fpumpは外部クロック周波数の1/2になります。
また、内蔵クロック周波数10kHzは入力電圧で変動するため、
指定したクロック周波数で動作させたい場合も、外部クロックを入力します。
<周波数を下げる方法>
OSC端子にコンデンサを接続することで、クロック周波数を下げることができます。
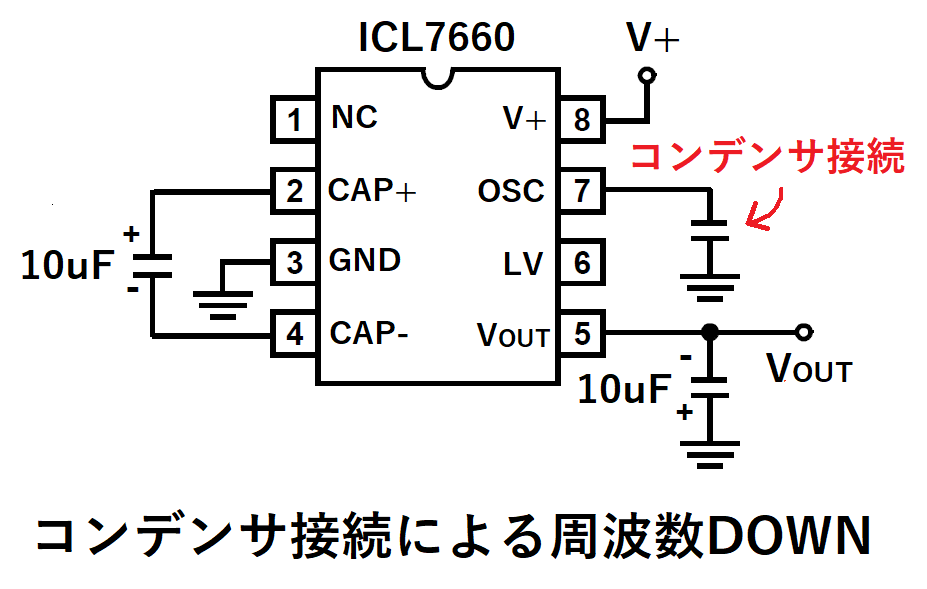
図に示すように、コンデンサ容量に応じてクロック周波数が低下します。
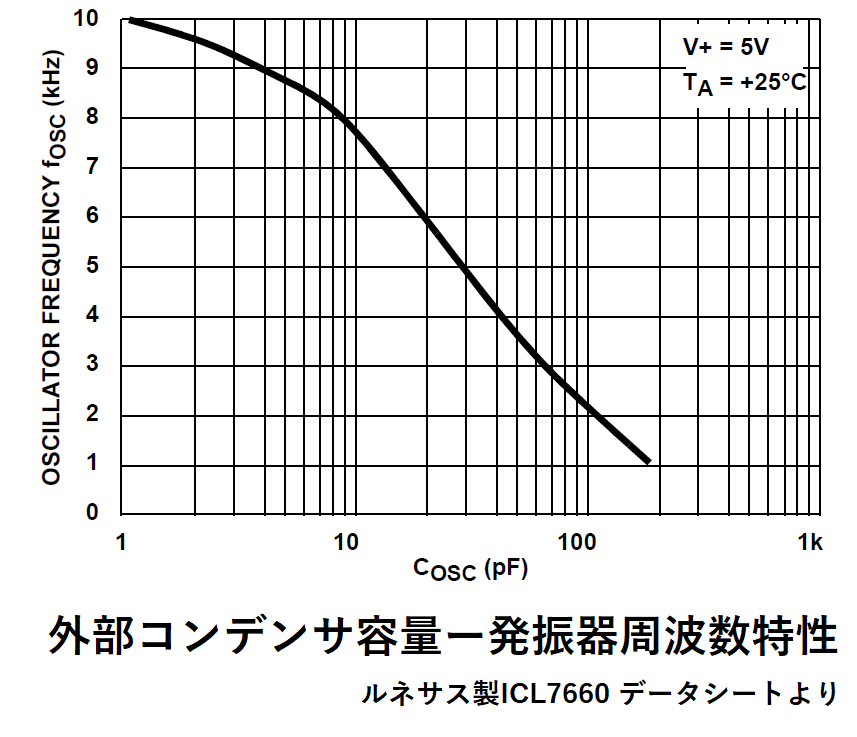
OSC端子への接続が長いと浮遊容量による影響で周波数が更に低下するので、
配線パターンは最短になるようにします。
周波数が低下すると、出力リップルが増加し、出力インピーダンスも増加します。
この時、周波数を下げた分、C1とC2の容量を増やすことで、これらの増加を抑えることができます。
例えば、100pFのコンデンサを接続すると、
発振器周波数が10kHz→約2kHzと1/5に低下するため、
C1とC2の値を5倍(50μFは無いので47uF)に増やします。
但し、高容量で、耐圧が高いMLCCは数が少なく、
電界コンデンサを使用した場合、ESRが10Ω程度とかなり大きくなる為、
再び、リップルやインピーダンスを増やす方向に働いてしまいます。
チャージポンプ回路の動作波形
負電圧回路と倍電圧回路の動作波形を示します。
<負電圧回路>
入力電圧Vin=5V時の起動波形です。
C1電圧のスイッチング毎に出力電圧Voutが徐々に変化し、-5Vになっています。
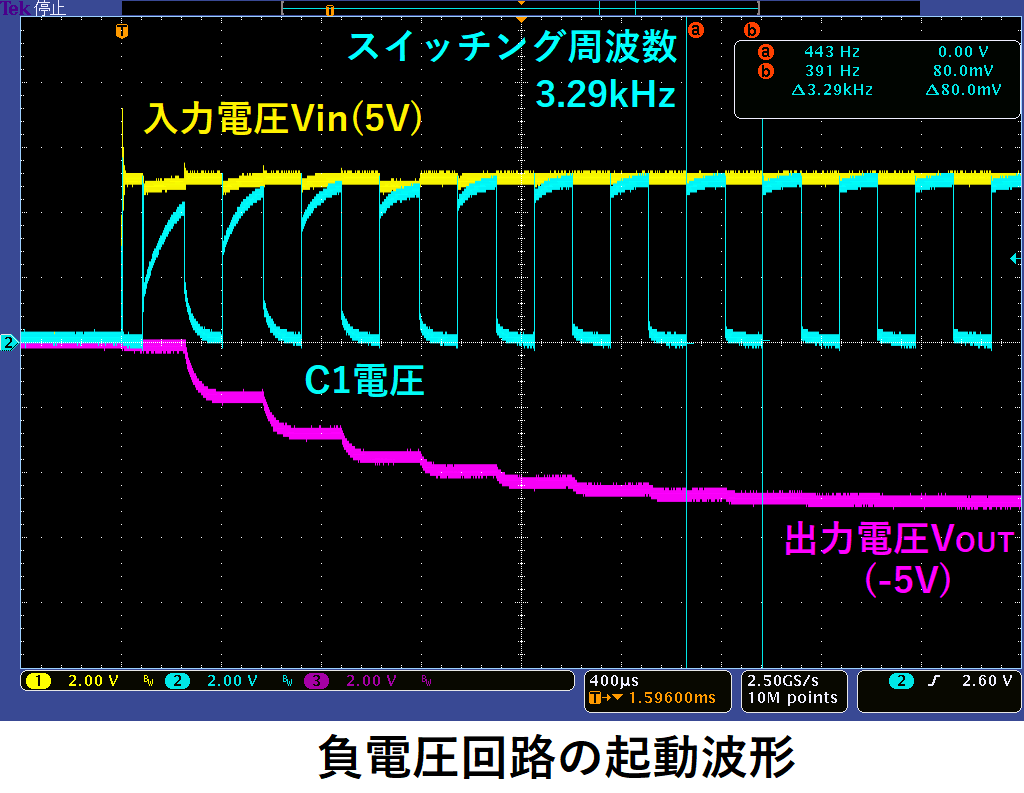
この時のスイッチング周波数は3.29kHzです。
データシートには発振器周波数10kHzとあるので、
スイッチング周波数はその半分の5kHzになると思うかもしれませんが、
入力電圧によって発振器周波数は変化します。
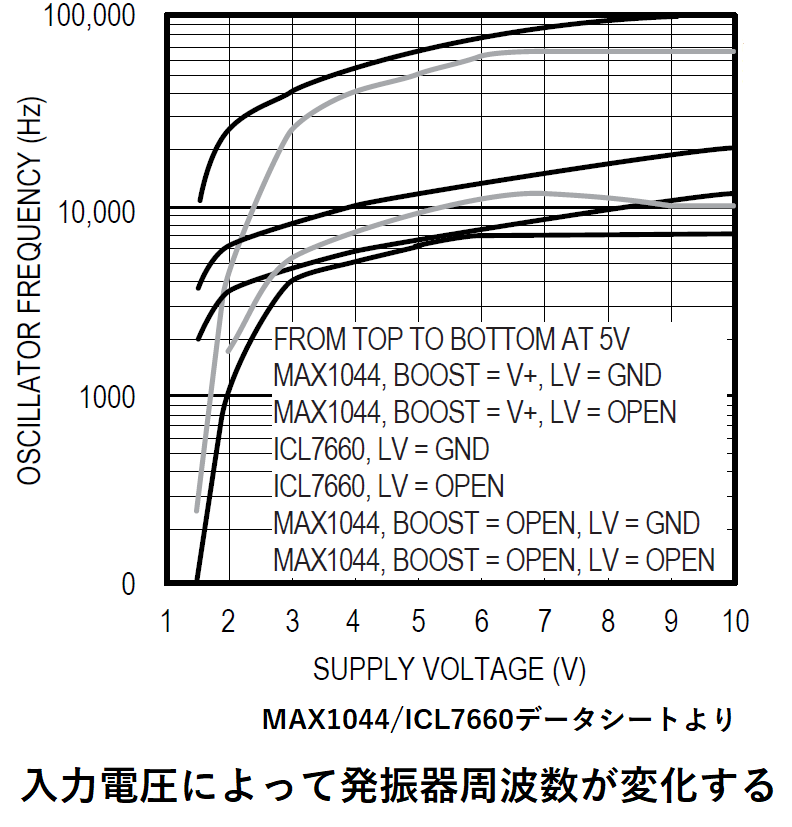
この特性グラフより、入力電圧10Vでは発振器周波数は10kHzですが、
5Vだと7kHz程度に低下していることがわかります。
(ちなみにVin=10V時のスイッチング周波数を測定したころ、4.35kHzでした)
この特性についてはメーカー各社で違うので注意が必要です。
出力電圧について、AC成分だけ測定したリップル電圧波形を示します。
負荷(出力電流)の増加によって、リップル電圧が大きくなり、
電圧降下も増えています。
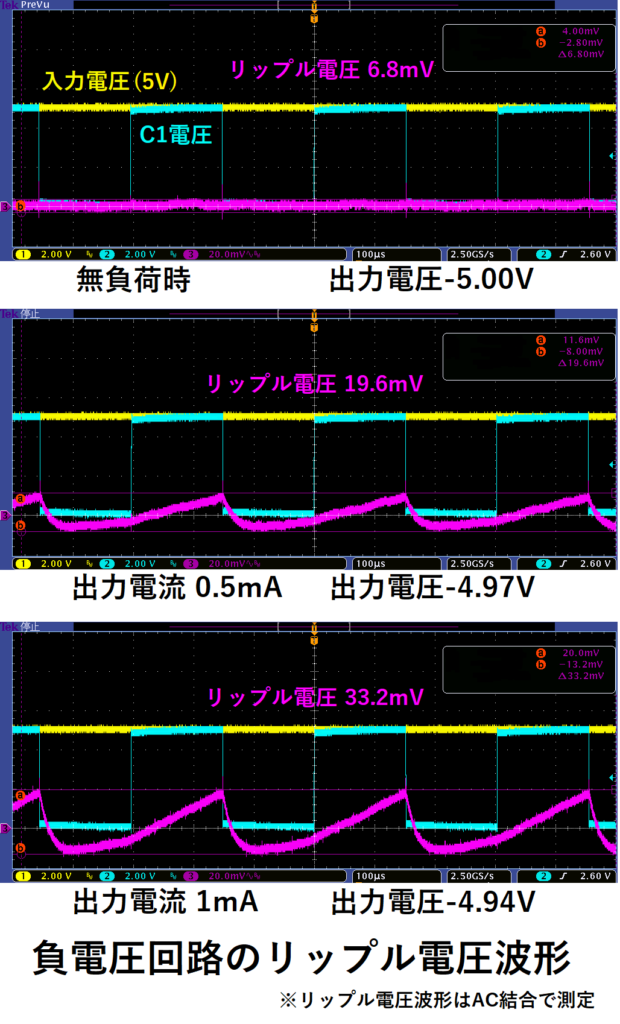
先程計算したリップル電圧に比べ、測定値が大きい理由は、
周波数fPUMPが小さくなっている事や、
Cの容量許容差などが影響していると考えられます。
この測定結果より、出力インピーダンスRoは
出力電流1mA時の電圧降下が60mVなので、
Ro=60mV/1mA=60Ω
であることがわかり、計算値の68Ωに近い値となっています。
<倍電圧回路>
入力電圧Vin=5V時の起動波形です。
C1電圧のスイッチング毎に出力電圧が徐々に増加し、約10Vになっています。

無負荷時でも出力電圧が9.95Vと、2倍の10Vにならないのは、
ダイオードD1,D2による電圧降下の影響です。
使用した新電元工業製ショットキーダイオードM1FH3のデータシートを見ると
順方向電圧VF=0.2V(IF=0.1A時)です。
このVF値はダイオードに100mA流した場合の値であり、
ここでは1mA程度と小さいため、実際のVFはかなり小さいと考えられます。
この事から、数mAレベルの出力電流なら、ほぼ2倍の電圧を得る事ができます。
負電圧回路と同様に、負荷の増加によって、
リップル電圧や電圧降下が増えているのがわかります。

出力インピーダンスについては、
出力電流1mA時の電圧降下が9.95ー9.77=0.18Vなので、
Ro=0.18V/1mA=180Ω
となりました。
★基板の部品交換や修正で役立つ工具類を紹介しています。