この記事でわかること
・コア形状とサイズの選定
・巻き数と線径の決め方
・トランス損失(鉄損、銅損)の計算方法
前回、スイッチング電源のトランス設計方法として、
フライバック・コンバータに使用する場合について解説しました。
フライバックとフォワードではトランスの動作が異なります。
フライバックがトランスにエネルギーを蓄えるチョークコイルとしての役割も担うのに対し、
フォワードでは、トランス本来の機能である電圧変換のみを行い、
エネルギーを蓄える役割は二次側に設けるチョークコイルが担います。
このため、トランス設計もフライバックとは違うことから、
本記事では、フォワード・コンバータ用のトランス設計方法を説明します。
トランス設計手順
以下の順番でトランスの各種仕様を決めていきます。
1.コアの選定
2.巻き数比Np/Ns
3.一次側巻き数Np
4.二次側巻き数Ns
5.巻線の線径
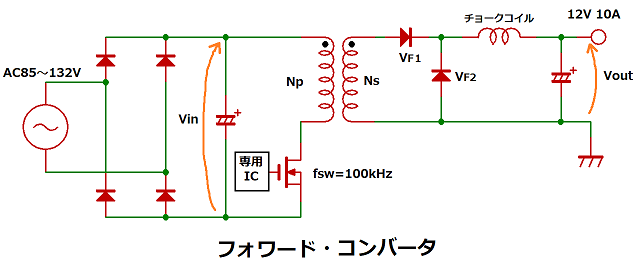
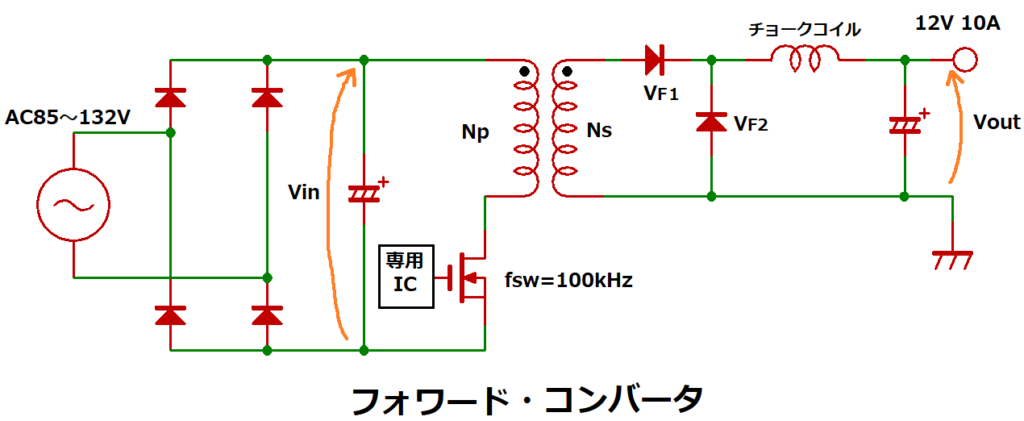
ここでは、以下に示すフォワード・コンバータに使用するトランスを例にします。
(以下、フォワード電源と称します)
・電源仕様
入力:AC100V (AC85~132V) 50/60Hz
出力:DC12V/10A (120W)
スイッチング周波数:100kHz
効率:85%
コアサイズの選定
コアが対応できる出力電力は、コアの断面積と巻枠の面積で決まります。
出力電力 ∝ コアの実効断面積Ae × 巻線断面積Acw
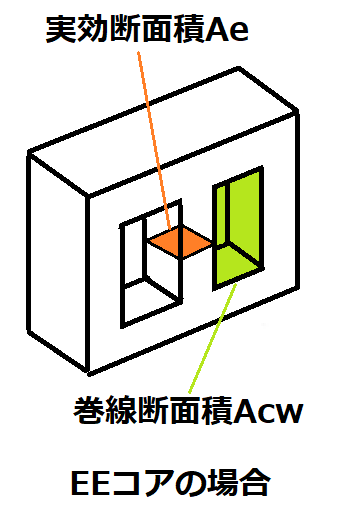
AeとAcwが大きいと太い電線を巻けるので、大電流を流すことができます。
以下に出力電力とコアサイズの目安を示します。
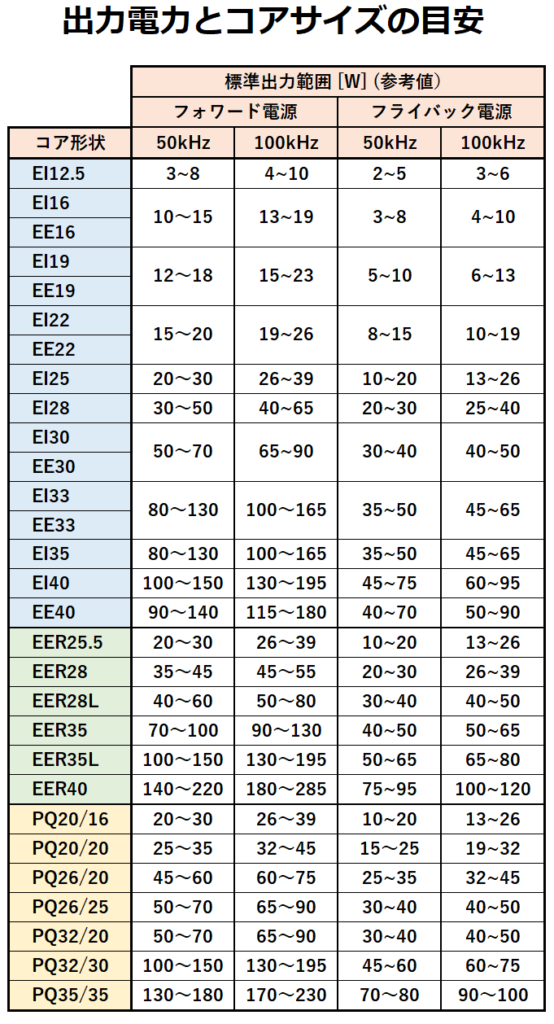
表にあるコア形状はスイッチング電源でよく利用されるものです。
EI、EE :安価だが巻線脚が矩形なので巻き難い
EER:巻線脚が円形のため巻き易いことから、最も良く使われる
PQ :磁気回路的に無駄が無く理想的な形状で、軽量化できる

スイッチング周波数はフォワード電源では通常、50kHz~100kHzの範囲で動作するため、
この表では、2つの周波数における出力電力が記載されています。
理論上は、スイッチング周波数が倍になれば、出力電力も倍になる筈ですが、
FETのスイッチング損失が増えるため、実際の出力電力は表のように
50kHz→100kHzにした場合、1.2~1.3倍程度となります。
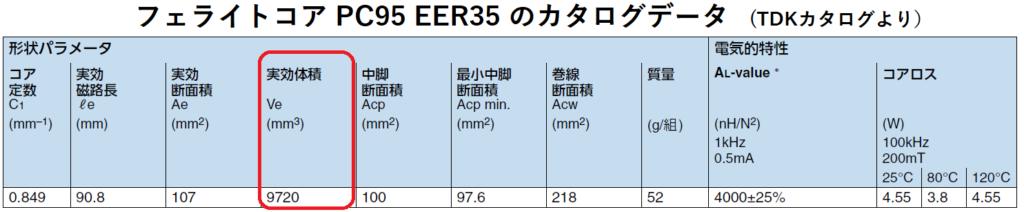
本例の出力電力は120Wなので、EER35を選定します。
理想的にはPQコアが良いのですが、EERの方が巻き易く、安価なので試作に向いています。
コア材質の選定
抵抗に電流を流すことで、抵抗に電圧が発生するのと同様に、
コアに磁界Hを加えることで、コア内に磁束Φが発生します。
磁界Hはコアに巻いた電線に電流を流すことで発生します。
磁束Φとは磁力線の本数であり、この本数が多い程、磁力が大きく、強い磁石と言えます。
コア材の性能を占めす指標として使われる磁束密度Bは、
コアの単位面積あたりの磁束(Φ=B×Ae)であることから、Bは大きい方が望ましいです。
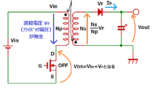
このBとHの関係を示すB-H曲線において、
フォワード電源はコアに流す電流が一方向なので、
Hは+の範囲でしか移動しません。
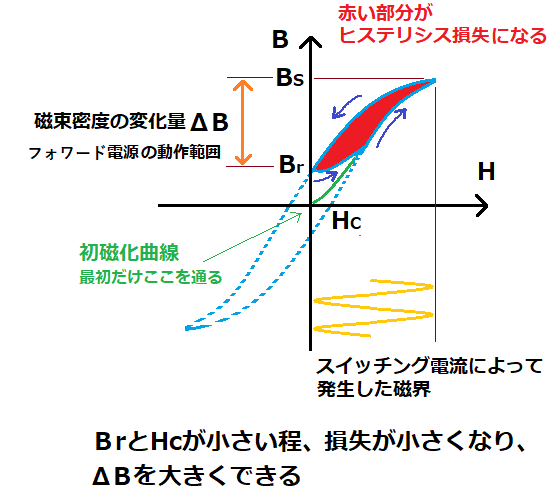
このため、電源動作時、Bは図に示すようなループ上を移動します。
このとき、コアの特性上、Hがゼロ(つまり、電流ゼロ)でもBはゼロになりません。
これを残留磁束密度Brと呼びます。
また、Hを増やしても、Bが増えなくなる限界を飽和磁束密度Bsと呼びます。
従って、磁束密度BはBsとBrの間で変化し、
この変化量ΔB=BsーBrが大きい程、大きな電力を伝えることができます。
また、コアで発生するヒステリシス損失は、B-H曲線が囲む面積に相当するため、
保持力Hcと残留磁束密度Brが小さい方がロスが少なく良い材質と言えます。
(この後で出てくるコアロス(鉄損)は、このヒステリシス損と渦電流損が主な成分です)
本例では、TDK製スイッチング電源用フェライトコアPC95を選定しました。

巻き数比Ns/Np
トランスの一次巻き数Npと二次巻き数Nsの比を求めます。
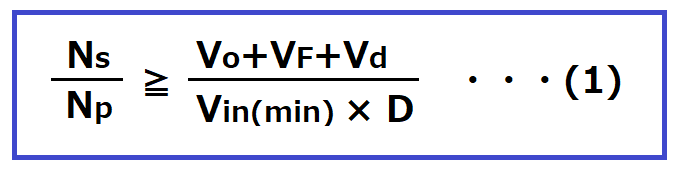
Vo:出力電圧[V]
VF:二次側整流ダイオードVF1の順方向電圧[V]
Vd:ダイオード以外の二次側電圧降下[V] (配線ドロップ等)
Vin(min):入力電圧の最小値[V]
D:ONデューティー
一次側FETのON時間/スイッチング周期の比です。
フォワード電源の場合、 通常は0.5を超えないように設定する(※1)ので、
ここでは最低入力電圧時に最大出力となるD=0.45にします。
Vinが最小値である理由ですが、
入力電圧が低い時でも出力電圧が維持できる巻き数比にする為です。
本例の場合、AC入力をブリッジダイオードで全波整流後、
コンデンサで平滑されたDC電圧がVinになります。
このDC電圧にはリップル成分があるので、その下限値をVin(min)とします。
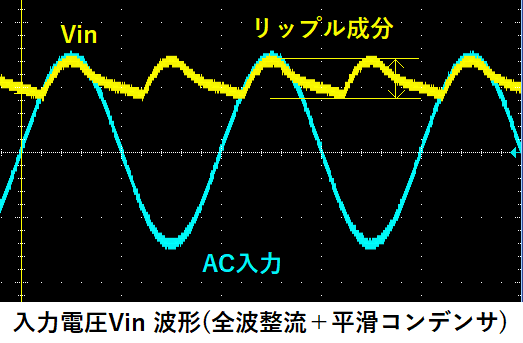
リップルの大きさは平滑コンデンサの容量が大きい程、小さくなり、
負荷電流が大きい程、大きくなります。
負荷電流が流れてもリップルを小さくするため、高容量のコンデンサを使用しますが、
大きすぎると、起動時の突入電流が増大し、
ブリッジダイオードの定格を超えると壊れてしまいます。
(このため、突入電流防止用にサーミスタ等を設ける場合もあります)
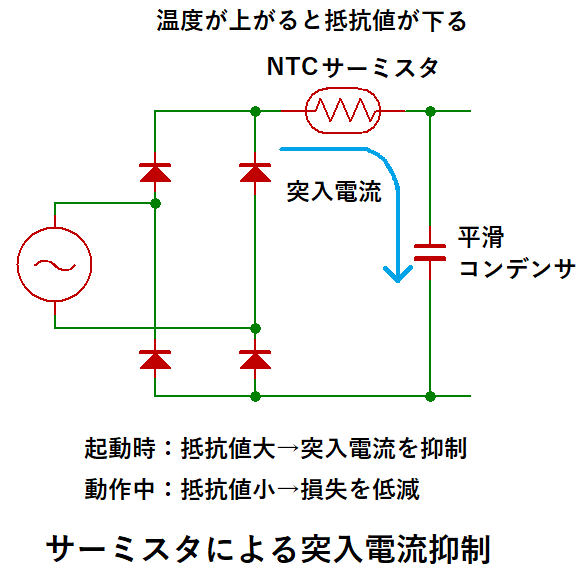
ここでは、リップルによる電圧降下を10%にした場合を想定し、
AC波形のピーク値(実効値×√2)の90%をVin(min)とします。
ブリッジ整流回路のリップル電圧の算出については下記記事で解説しています。
<計算例>
本例の最低入力条件であるAC85Vの場合、
Vin(min)=85×√2×0.9=108V
整流ダイオードの順方向電圧が0.55V、
それ以外の配線ドロップ等による電圧降下を0.5Vとすると、巻き数比は
(Ns/Np)≧ (Vo+VF+Vd)/(Vin×D)
=(12+0.55+0.5)/(108×0.45)
≒0.27
<参考:(1)式になる理由>
トランスの一次側電圧Vp、二次側電圧Vsとすると
Ns/Np=Vs/Vp
Vpは入力電圧VinがONデューティーDの期間だけ印加されるので、
Vp=Vin×D
整流ダイオードの順方向電圧VFとその他のロス分をVdとすると、出力電圧Vsは
Vs=Vo+VF+Vd
なので、
Ns/Np=(Vo+VF+Vd)/(Vin×D)
となります。
≧が付くのは、巻き数比Ns/Npが計算値より小さいとVoが維持できなくなる為です。
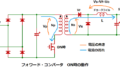
※1: Dが0.5を超えない様にする理由
ON時間がOFF時間より長くなると、
トランスの一次側電流がゼロにならないうちにONしてしまうことで電流が増大していき、
コアが磁気飽和(※2)を起こしてしまいます。
このため、フォワード電源ではOFF時に一次側電流が早く減少するように
リセット回路(スナバ回路とも呼ばれる)を設けて電流を逃がすようにしたり、
トランスにリセット巻線を設けることで、エネルギーを放出させるようにしています。
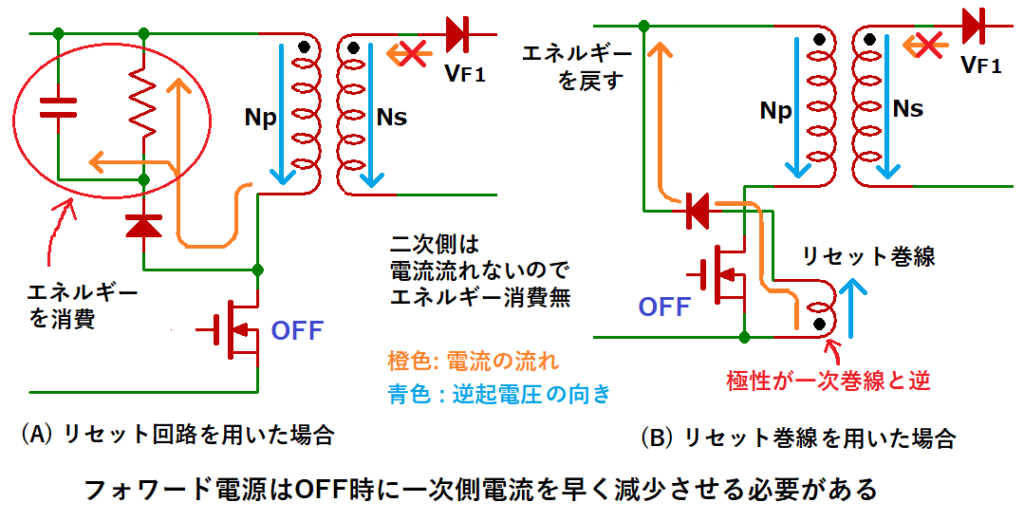
記事の最初でフォワード電源用のトランスはエネルギーを蓄えないと言いましたが、
実際のトランスコイルには電圧変換に寄与しない漏れインダクタンス成分があり、
これがチョークコイルとして働くことで、エネルギーを蓄えます。
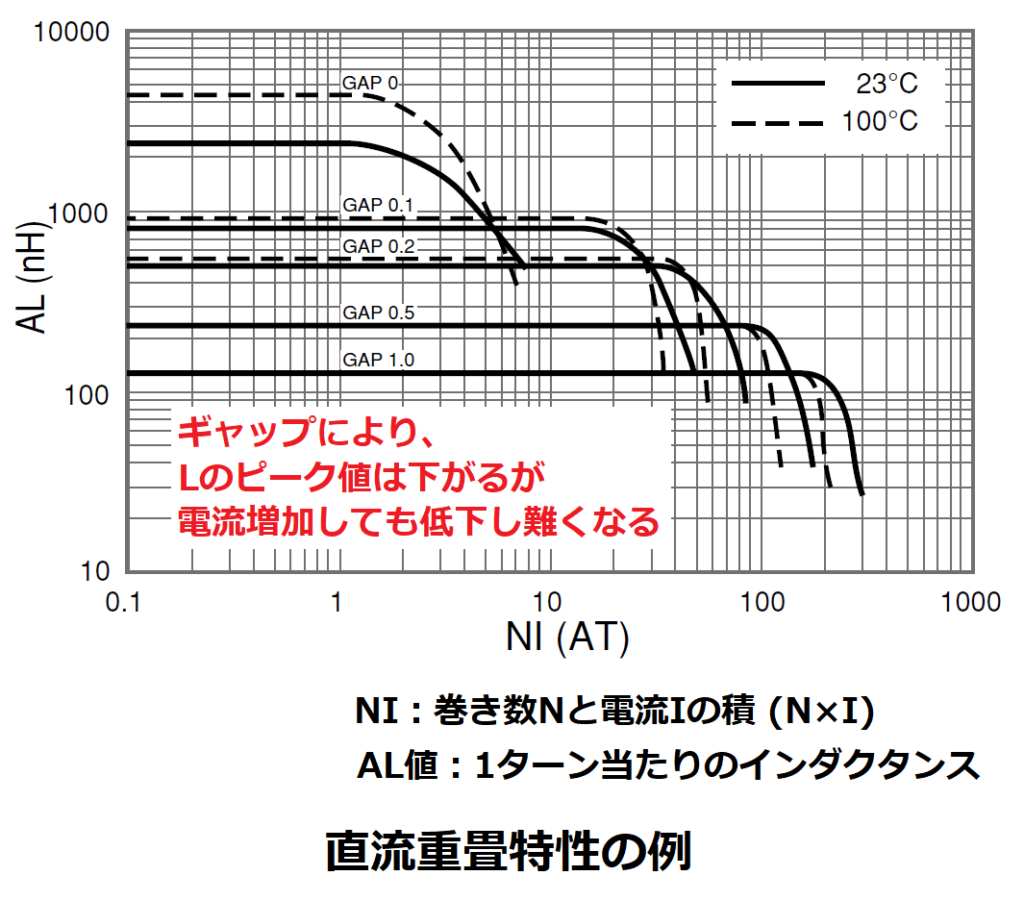
また、大電流を流してもコアが磁気飽和を起こしにくいように、コアにギャップを設けた場合、
これが漏れインダクタンスを増加させてしまうため、
上記の様なエネルギーを逃がす仕組みが必要となります。
※ギャップについては、フライバック電源用トランスの記事で解説しています。

※2: 磁気飽和について
磁気飽和とは、電流を多く流すことでインダクタンスLが低下してしまう現象(直流重畳特性)で、
コイルとして機能しなくなる(ただの電線と同じになる)ことで、回路がショートする恐れがあります。
磁気飽和が発生する仕組みは以下の通りです。
L=N×Φ/I=N×B×Ae/Iより、
巻き数Nと断面積はAeは固定値なので、
インダクタンスLは磁束密度Bに比例し、電流Iに反比例します。
このため、先程のB-H曲線より、Iがある程度増加するとBが増えなくなので、Lが低下します。
コイルのインピーダンスは2π×f×Lです。(fはスイッチング周波数)
Lが減少するとインピーダンスが低下し、
流れる電流が更に増加することで、Lが急激に低下します。
一次側巻き数Np
一次巻線の巻き数Npは以下の式より求めます。
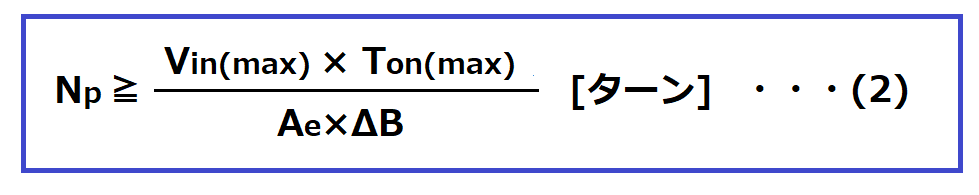
Vin(max):入力電圧の最大値 [V]
Ton(max):一次側FETのON時間の最大値 [s]
=(1/スイッチング周波数[Hz])×最大ONデューティ
Ae:コアの実効断面積 [m2]
ΔB:磁束密度の変化量 [T]
=( Bs(飽和磁束密度) ー Br(残留磁束密度) )×0.6~0.8
ここで0.6~0.8を掛けているのは、過負荷時に電流が多く流れても、
飽和磁束密度Bsを超えないようにするためマージンをとっています。
(2)式で、入力電圧VinとON時間Tonが最大にしている理由は、
入力エネルギーが最大となる場合でも、コアが磁気飽和しないように巻き数を確保するためです。
<補足>
(2)式を変形すると、Np×Ae×ΔB=Vin×Tonなので、
Vin×Tonが大きい時にNpが小さいと、ΔBが増大します。(Aeは固定値なので)
ΔBが増大する事は、飽和磁束密度Bsを超えることを意味し、磁気飽和が発生します。
<計算例>
本例のNpを求めると、
Vin(max)は、AC132[V]×√2≒187[V]
Ton(max)=(1/100kHz)×0.45=0.0045[ms]=4.5×10-6[s]
コアEER-35の実効断面積はカタログより、
Ae=107[mm2]=107×10-6[m2]
ΔBはコア材PC95について、温度100℃の値(Bs=410mT、Br=60mT)から計算しました。
ΔB= (410ー60) ×0.6=210[mT]
Np=Vin(max)×Ton(max))/(Ae×ΔB)
=187×4.5×10-6/(107×10-6 ×0.21)
≒37.4 [ターン]
従って、Npは38ターン以上にする必要があります。
<参考:(2)式になる理由>
ファラデーの法則より、
V=N×dΦ/dt Φは磁束(磁力線の本数)
公式的にはV=ーN×dΦ/dtと、マイナス符号がつきますが、
磁束の流れを妨げるための逆起電圧を意味するものなので、
ここでは符号が無くても構いません。
式を変形すると、
V×Δt=N×ΔΦ
磁束Φと磁束密度Bの関係は、Φ=B×Ae なので、
上記の式と合成すると、
V×Δt=N×ΔB×Ae
となり、式を変形すると
N=V×Δt/(Ae×ΔB)
となります。
(2)式で≧が付くのは、Npが計算値より小さいとΔBが増えてBsを超えてしまう為です。
二次巻き数Ns
算出した巻き数比と、一次巻き数から、二次巻線の巻き数Nsを求めます。

<計算例>
本例のNsを求めると、
Ns≧Np×(Ns/Np)=38×0.27=10.26
ここで、Ns=11とした場合、巻き数比からNpを逆算すると、
Np≦Ns×(Np/Ns)=11 ×(1/0.27)≒40.7
となるので、Np=38でOKです。
また、巻き数比を求めた時の条件である
Ns/Np≧0.27を満足するか確認します。
Ns/Np=11/38=0.289≧0.27
となるのでOKです。
最低入力電圧と磁束密度の確認
求めた巻き数Np、Nsにした場合の、
出力電圧Voを維持できる最低入力電圧Vin(min)を計算し、
定格入力電圧範囲内であることを確認します。
巻き数比を求める式(1)を変形し
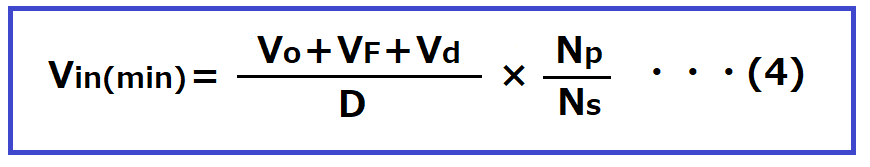
<計算例>
Vin(min)=(12+0.55+0.5)/0.45×38/11
≒100.2 [V]
本例の仕様では入力電圧が最も低くなる条件はAC85Vの時であり、
この時のVinは一次巻き数の算出時に求めた108Vになるので、
計算したVin(min)より高いことから、出力電圧Voを維持できます。
次に、最大出力(入力電圧及びデューティが最大)時に
飽和磁束密度Bsを超えないか確認します。
一次巻線の巻き数を求める式(2)を変形し、

<計算例>
ΔB=Vin(max)×Ton(max)/(Ae×Np)
=187×4.5×10-6/(107×10-6 ×38)
≒0.207 [T] =207[mT]
最大磁束密度Bmは
Bm=ΔB+Br
=207+60=267[mT]
となり、飽和磁束密度Bs (410mT)を超えないことが確認されました。
巻き線の損失
巻き数が決まったので、線径を決めることになりますが、
そのためには、巻線での損失(銅損)をどれくらいに抑えるかを決めておく必要があります。
銅損Pwの算出は以下の手順で行います。
1.トランスの許容損失(トータルロス)Pmを決める
2.コア損失(鉄損)Pcを算出する
3.PmーPcから巻線での損失(銅損)Pwが求まる
※フェライトコアは酸化鉄を主成分としているので鉄の一種であり、
そのコアに起因する損失なので鉄損と呼ばれます。
また、巻線は銅からできているので銅損と呼びます。
ここでは、定格電圧入力時の条件で計算します。
<1.トランス損失Pm>
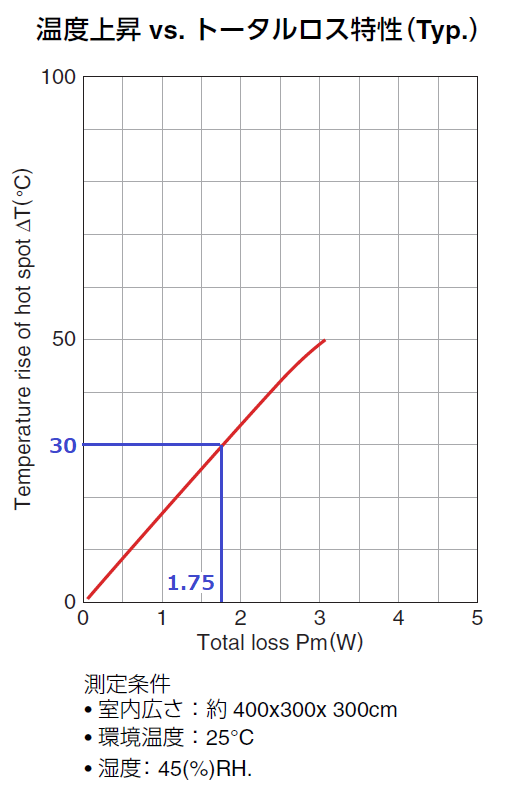
自然空冷時のトランスの温度上昇目標値を30℃とすると、
コアEER35のカタログ記載の温度上昇ートータルロス特性グラフより、
トランス損失Pmは1.75Wまで許容できます。
<2.コア損失(鉄損)Pc>
コア損失Pcは次の式となります。
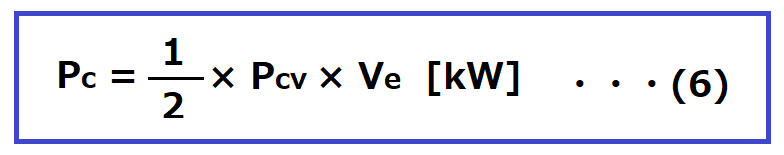
Pcv:単位体積あたりのコア損失[kW/m3]
Ve:コアの実効体積[m3]
この式で、1/2にしている理由ですが、
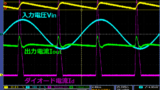
Pcvはコア材のカタログに記載されているPcvーBm特性グラフから求めますが、
このグラフのPcvの値は磁界Hが±成分のある正弦波を加えた場合になります。
つまり、トランスのコイルに±電流を流した時の損失であり、
先程のBーHカーブの破線部分を含めた面積に相当します。
フォワード電源では先述した通り、
B-Hカーブの片側しか利用しない為、半分にします。
PcvーBm特性グラフからPcvを求めるため、
定格動作時の最大磁束密度Bmを計算します。
Bm=ΔB+Br
ΔB:磁束密度の変化量(定格入力時)
Br:残留磁束密度
本例では、コア材PC95のカタログ記載の60mTになります。
ΔBは一次巻き数の式(2)を変形し、
ΔB=Vin×Ton/(Ae×Np)
=Vin×(D/f)/(Ae×Np)
Vin:入力電圧(定格入力時)[V]
巻き数比の算出時と同様、リップルによる電圧降下を考慮し、
AC波形のピーク値(実効値×√2)の90%程度とします。
定格入力AC100Vの場合、
Vin=100×√2×0.9=127V
D:デューティ(定格入力時)
巻き数比の式(1)を変形し、
D=(Vo+VF+Vd)/Vin ×Np/Ns
=(12+0.55+0.5)/127×38/11
≒0.35
f:スイッチング周波数[Hz] 100kHz
Ae:コアの実効断面積 [m2] 107×10-6 [m2]
Np:一次巻き数 38[T]
従って、
ΔB=Vin×(D/f)/(Ae×Np)
=127×(0.35/100×103)/(107×10-6 ×38)
≒0.109[T]=109[mT]
Bm=ΔB+Br
=109+60=169[mT]
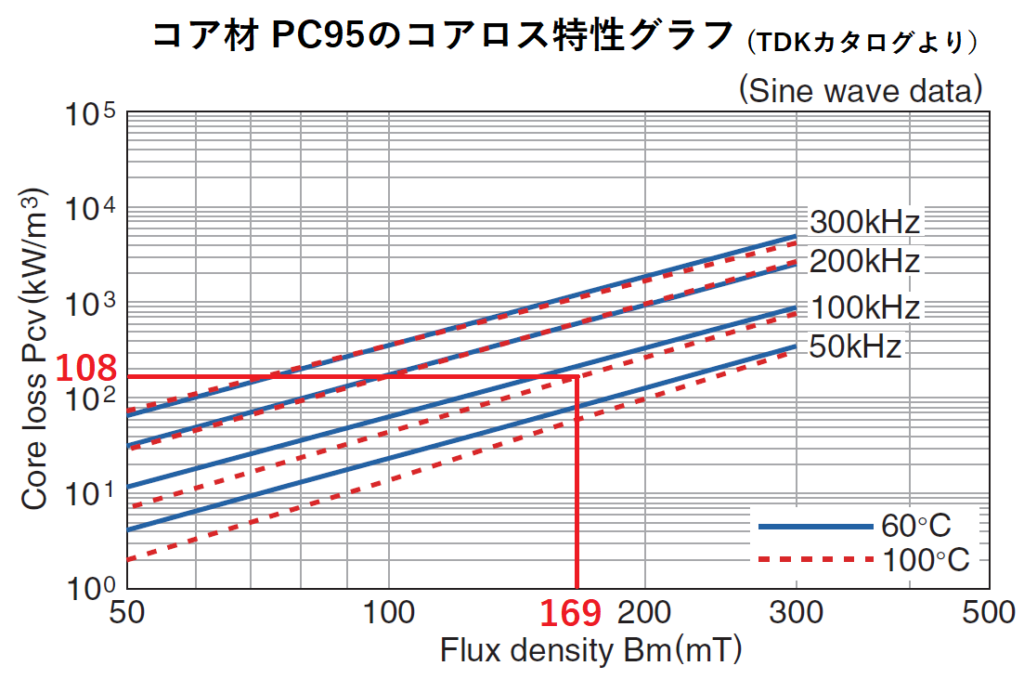
Bm=169mT、スイッチング周波数100kHz、周囲温度100℃とした場合、
コア材PC95のカタログ記載のPcvーBm特性より、
Pcv=108[kW/m3]
となります。
コアの実効体積Veはコア(EER35)のカタログより、
Ve=9720[mm3]=9720×10-9[m3]なので、
コア損失Pcは、
Pc=(1/2)×Pcv×Ve
=(1/2)×108× 9720×10-9
≒525×10-6[kW]=0.525[W]
<3.銅損Pw>
トランスの損失はコア損失Pc(鉄損)と巻線の損失Pw(銅損)の合計なので、
Pm=Pc+Pw
従って、銅損Pwは以下の値以下にする必要があります。

Pw=1.75ー0.525
=1.225[W]
巻線損失は一次巻線と二次巻線で半分ずつ消費されるとした場合、
各巻線の許容損失Pwireは
Pwire=Pw/2
=1.225/2≒0.613[W]
となります。
線径
巻線の線径Φは、
円の面積の公式S=π × (Φ/2)2を変形した下記式から求めます。
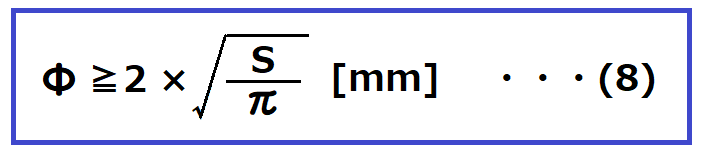
Φ:巻線の線径[mm]
S:巻線の断面積[mm2]
巻線の断面積Sは下記式で示す面積以上にする必要があります。
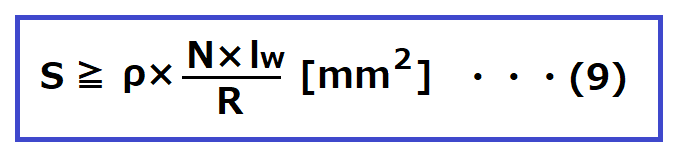
ρ:銅の抵抗率[Ω・mm]
ここでは100℃の場合の2.3×10-5[Ω・mm]を使用します。
N:巻線の巻き数[ターン]
lw:平均巻線長[mm]
巻線をボビンに1ターン巻いた時の巻線長の平均値です。
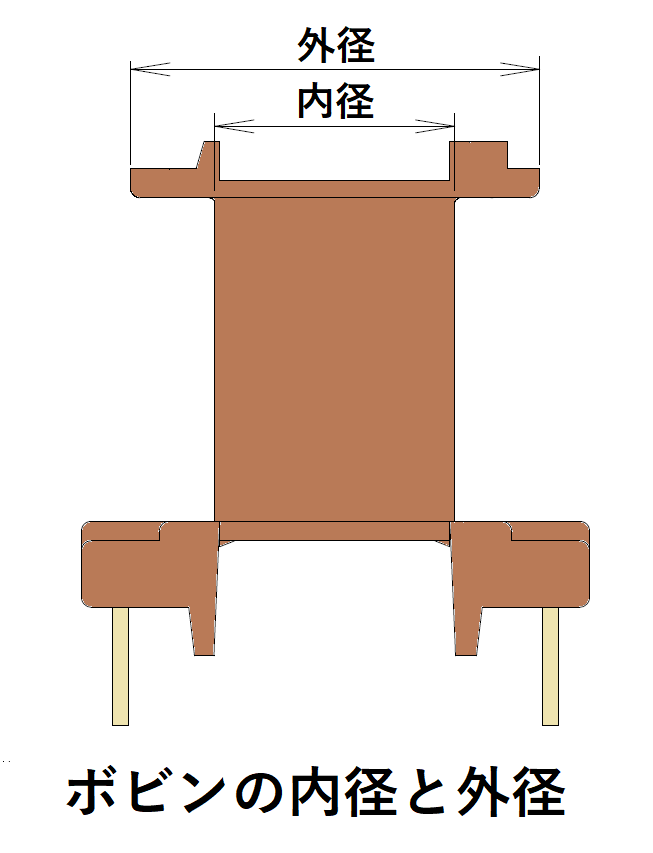
ボビンの内径と外径が判れば、その平均径から、
円周=平均径 × πより求めます。
ここでは概算のため、コアの内径と外径の平均値とします。
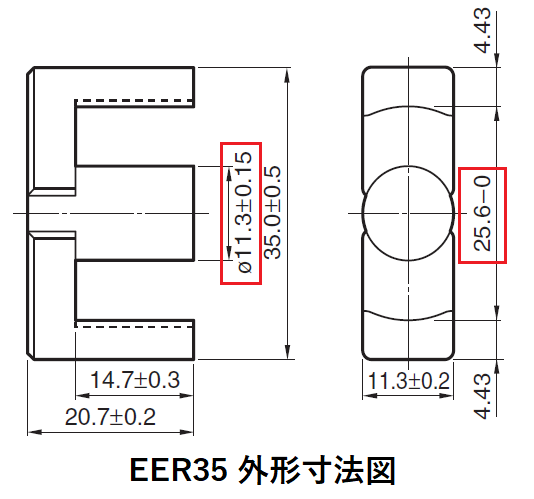
EER35の外形図より、内径11.3mm、外径25.6mmなので、
その平均値18.45mmを用いて、
Iw=18.45 × π≒57.9mm
R:巻線の抵抗値[Ω]
先程求めた巻線の許容損失以下にするために、
抵抗値を以下の値より小さくします。

Pwire:巻線の許容損失[W]
本例では、0.608[W]になります。
I(rms):巻線電流の実効値[A]
一次巻線、二次巻線、それぞれ算出します。
以上から、一次巻線、二次巻線の線径Φを求めるために、
各巻線に流れる電流の実効値I(rms)を計算します。
<一次側巻線の場合>
巻線に流れる電流波形を矩形波として近似した場合、
実効電流I(rms)は以下の式となります。
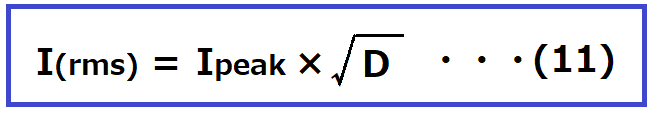
D:入出力定格時のデューティ
本例では、先程求めた0.35になります。
Ipeak:ピーク電流[A]
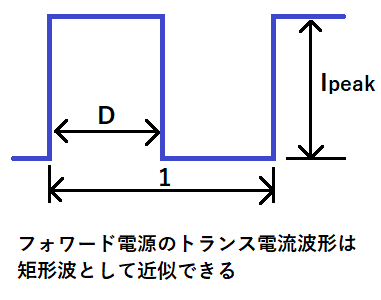
一次側巻線のピーク電流Ipeakは下記の式で求められます。
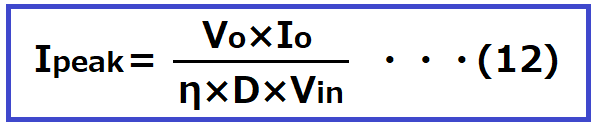
Vo:出力電圧[V] 12V
Io:出力電流[A] 10A
η:フォワード電源の効率 ここでは、85%と設定
D:入出力定格時のデューティ 0.35
Vin:定格入力電圧[V] 127V
よって、
Ipeak=Vo×Io/(η×D×Vin)
=12×10/(0.85×0.35×127)
≒3.18[A]
実効電流I(rms)は(11)式より
I(rms)=Ipeak×√D
=3.18×√0.35
≒1.88[A]
巻線抵抗Rは(10)式より
R≦Pwire/I(rms)2
= 0.613/1.882
≒0.173[Ω]
断面積Sは(9)式より
S≧ρ×(Np×lw)/R
=2.3×10-5×(38×57.9mm)/0.173
≒0.29 [mm2]
線径Φは(8)式より
Φ≧2×√(S/π)
=2×√(0.29/π)
≒0.60[mm]
従って、一次巻線の線径は0.60mm以上になりますが、
線径が0.5mmを超えると、硬くて巻き難くなります。
また、周波数100kHzの場合、表皮効果の影響を低減するには、
0.48mm以下にする必要があります。(※3)
ここでは、線径が0.45mmの線材を2本並列巻きにします。
断面積は(0.45/2)2 × π × 2本≒0.32mm2となり、
必要な断面積0.29mm2より大きいのでOKです。
<二次巻線の場合>
二次巻線の実効電流Is(rms)は、先程求めた一次側巻線の実効電流値Ip(rms)から求めます。
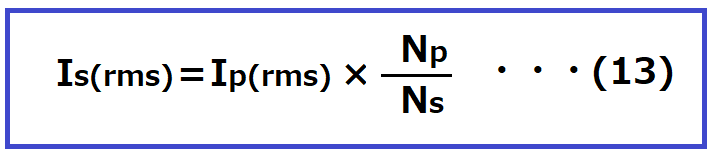
よって
Is(rms)=1.88×(38/11)
≒6.49A
巻線抵抗Rは(9)式より
R≦Pwire/Is(rms)2
= 0.613/6.492
≒0.015[mΩ]
断面積Sは(9)式より
S≧ρ×(Ns×lw)/R
=2.3×10-5×(11×57.9)/0.015
≒ 0.98[mm2]
線径Φは(8)式より
Φ≧2×√(S/π)=2×√(0.98/π)
≒1.1[mm]
従って、二次巻線の線径は1.1mm以上になりますが、
線径0.45を使用した場合の本数nは
n≧S/(π × Φ2/4) =0.98/(π×0.452/4)≒6.2
となり、7本となります。
ここまで本数が多いと束ねるのは大変なので、
リッツ線を使用すると良いです。

リッツ線は、細い素線を撚り合わせて1本にした電線です。
Φ0.2×35束を使用した場合、
断面積は(0.2/2)2 × π × 35本≒1.09mm2となり、
必要な断面積0.98mm2より太いので使用できます。
ここでの計算は、あくまで目安なので、
実際にはトランスを試作し、動作時の温度を測定し、
温度上昇の目標値以内であるか確認します。
巻線の温度は絶縁テープを介して熱電対で測定しますが、
それは、外側に巻かれている二次巻線の温度であり、
内側にある一次巻線の方が熱くなることを考慮し、マージンを取る必要があります。
また、コアのサイズ・形状によっては、巻線に熱電対をつけにくい為、
線径を変えて都度比較する際は、コアの温度を測定し、
その温度に10℃プラスした値を巻線温度の目安にできます。
※3:表皮効果の影響を低減できる線径の求め方
表皮効果による浸透深さδ[mm]は以下の式で計算できます。
δ=√(ρ/(π × f × μ))
ρ:抵抗率[Ω・mm]
f:周波数[Hz]
μ:透磁率[H/mm]
浸透深さとは、電流が表面電流の1/e(約0.37倍)まで減衰する距離です。
ここで、透磁率u=μ0×ur です。
u0:真空の透磁率 4π × 10-7[H/m]
ur:比透磁率
銅などの非磁性金属のurは、ほぼ1なので、
μ=μ0×ur≒μ0
=4π × 10-7[H/m]=4π × 10-10[H/mm]
銅の抵抗率ρ=2.3×10-5[Ω・mm]を代入すると、
以下の式に近似できます。
δ=76/√f
周波数100kHzの場合の浸透深さδは
δ=76/√f
=76/√(100×103)=0.24[mm]
従って、電線の半径を0.24mm以下にすれば、
表皮効果の影響を受けにくくすることができるので、
線径が0.24×2=0.48mmより細い巻線を使用する必要があります。
★トランスの作り方について解説しています。
★フォワード・コンバータのチョーク・コイル設計法を解説しています。
★試作時で役立つ工具類を紹介しています。