この記事でわかること
・平滑コンデンサ容量の決め方
・コンデンサのリップル電流の目安
・実測値、シミュレーション値との差について
整流回路はダイオードとコンデンサだけの簡単な構成ですが、
出力電圧はリップル成分を持ち、その大きさはコンデンサ容量や
負荷電流等によって変化するため、電圧値の算出が難しいです。

このため、整流回路の設計には次の2つの方法が一般的に用いられます。
・SPICE(回路シミュレーション・ソフト)を使用する方法
・O.H.Schadeのグラフを使用する方法
シミュレーションというと、敷居が高いイメージがありますが、
代表的なフリーソフトであるLTspiceを使えば、
比較的簡単に出力電圧波形を得ることができます。
もう一つのO.H.Schadeのグラフを用いる方法は、
80年以上前に考案されたものですが、今でも十分通用します。
この方法は、出力電圧とリップル成分を、どれくらいにするか決めた上で、
入力電圧と負荷抵抗等から算出したパラメータを基に、
グラフから必要なコンデンサ容量を求めることができます。
本記事では、O.H.Schadeのグラフを用いた整流回路の設計方法について説明し、
LTspiceによるシミュレーション値や、実測値との比較結果についても解説します。
O.H.Schadeのグラフ
O.H.Schadeのグラフには以下の3種類があり、
これらを組み合わせて使うことによって、コンデンサの選定に必要な
容量やリップル電流を求めることができます。
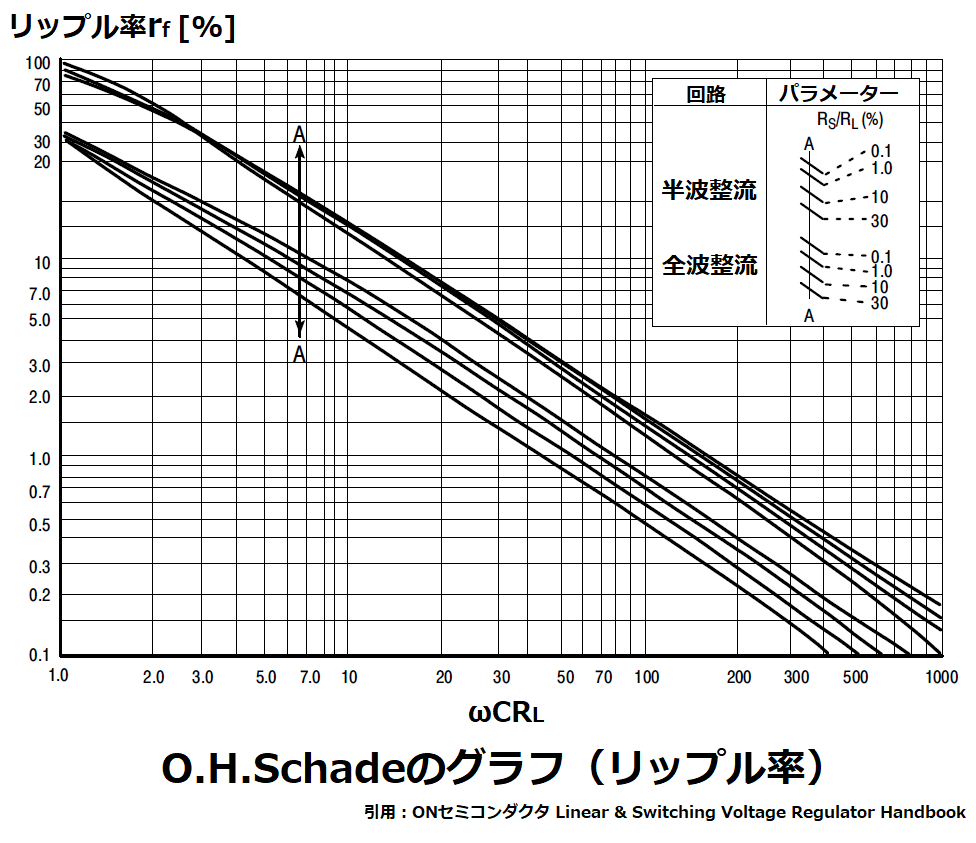
①リップル率rf(=リップル電圧(実効値)/DC出力電圧)
②DC出力電圧/AC入力電圧(最大値)の比 Vout/Vin
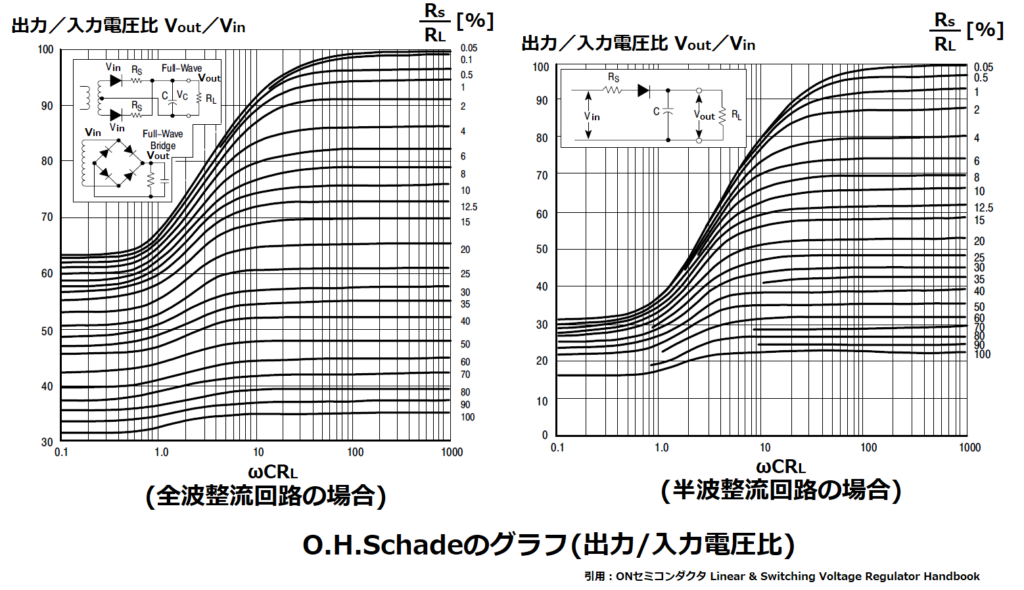
①②のグラフは、共に2つのパラメータωCRL、Rs/RLによって、値が決まります。
(ωは角周波数[rad/s]で、ω=2πf f:電源周波数(50Hz又は60Hz))
設計条件からリップル率、出力/入力電圧比、負荷抵抗RLを決め、
これらの条件を満たすωCRL、Rs/RLをグラフから読み取ることで、
コンデンサ容量Cと、内部抵抗Rsが求まります。
③ダイオード実効電流比Irms/Iave、ピーク電流比Ip/Iave
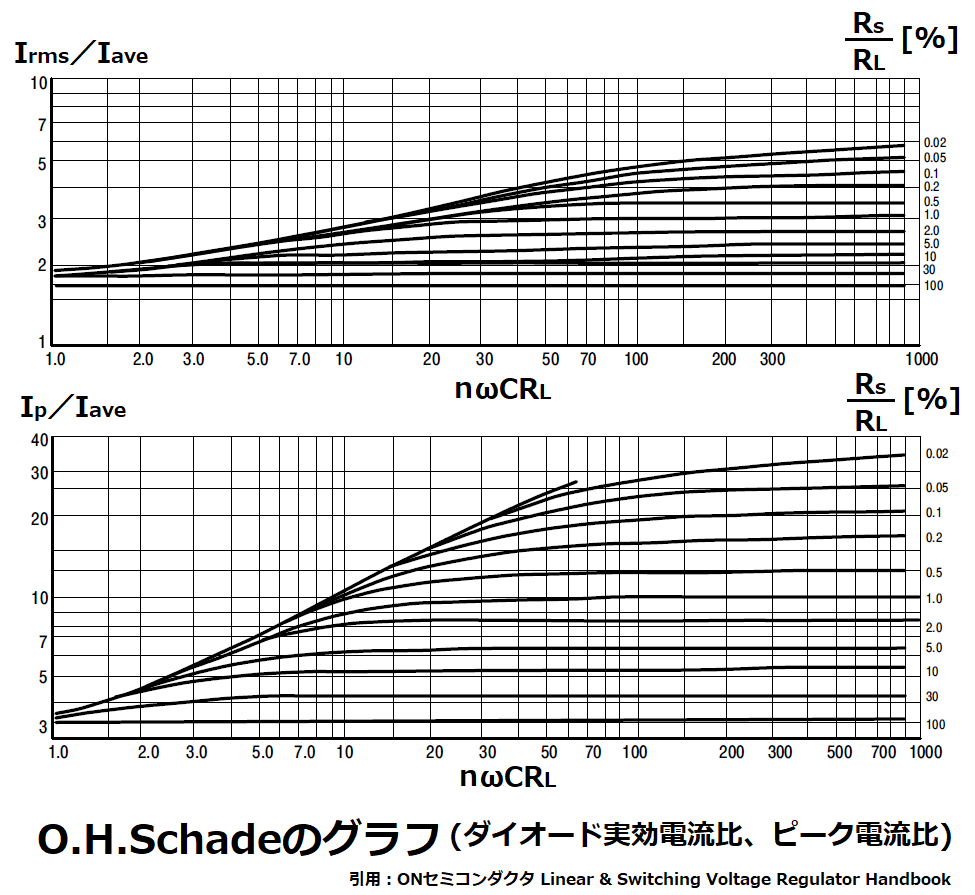
①②で決めたωCRL、Rs/RLを基にして、グラフから
整流ダイオードに流れる実効電流とピーク電流が求まることで、
ダイオードの選定に利用したり、コンデンサのリップル電流の目安がわかります。
必要なパラメーターを求める
O.H.Schadeのグラフでは、整流回路の平滑コンデンサ容量を求めるにあたり、
4つのパラメータ(Vin、Vout、RL、Rs)を使用します。
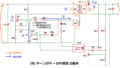
ここでは、以下の整流回路を例にして説明します。
例:入力電圧:AC100V 50Hz
出力電圧:134V ±7V
出力電流:300mA
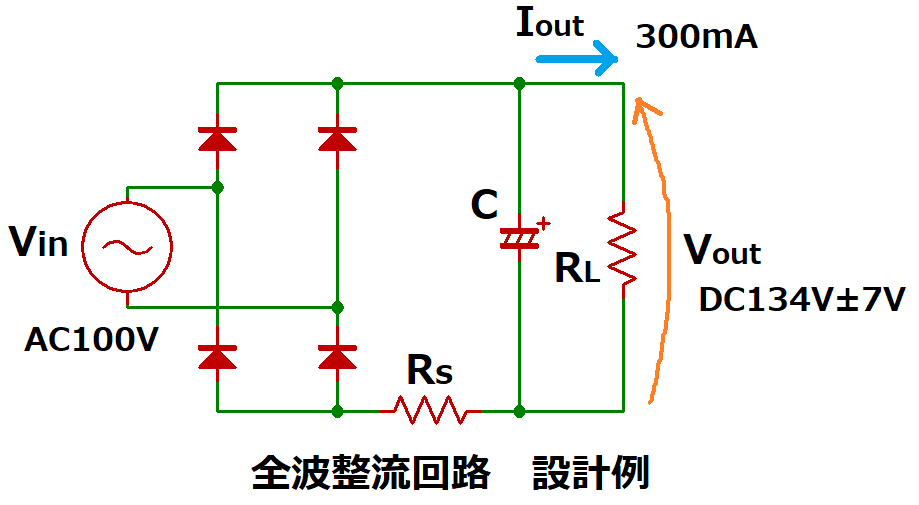
リップル電圧の振幅幅を±7Vにすることで、
出力電圧の下限値(127V)がピーク値(141V)の90%になるようにしています。
厳密にはダイオードの順方向電圧VFによる電圧降下があり、
ブリッジダイオードの場合、2個分となる2×VFだけ出力電圧が低下しますが、
ここでは簡略化のため無視しています。
・入力電圧Vin
整流回路への最大入力電圧(無負荷時)です。
O.H.Schadeのグラフを使用するための前提条件として、
入力電圧波形は正弦波である必要があり、Vinはそのピーク値となります。
AC100Vを入力する場合は、
Vin=100×√2=141V
となります。
・出力電圧Vout
DC出力平均電圧になります。本例では134Vです。
・負荷抵抗RL
整流回路に接続する負荷抵抗です。
出力電流をIoutとした場合、
RL=Vout/Iout
で求めます。
本例では、
RL=134V/0.3A≒447Ω
になります。
・内部抵抗Rs
電源入力から平滑コンデンサ間の抵抗成分になります。
具体的には、突入電流防止用の抵抗や、
トランスから電源入力する場合は巻線抵抗が該当します。
本例では、Rsが未定であることを前提として、
他のパラメータを基にグラフから求めます。
リップル率rfを求める
リップル率rfは以下の式となります。
rf=Vr(rms)/Vout ×100 [%] ・・・(1)
Vr(rms):リップル電圧の実効値
リップル電圧の振幅Vr(p-p)より、
Vr(rms)=Vr(p-p)/(2√2)・・・(2)
で求まります。
<計算例>
リップル電圧が±7Vなので、振幅Vr(p-p)=14V
リップル電圧の実効値Vr(rms)は(2)式より、
Vr(rms)=Vr(p-p)/(2√2)
=14/(2√2)≒4.95[V]
リップル率rfは(1)式より、
rf=Vr(rms)/Vout
=4.95/134≒0.037=3.7[%]
になります。
<(2)式になる理由>
リップル電圧波形を正弦波に近似して考えると、
リップル電圧のピーク値Vrpは、
Vrp=√2×Vr(rms)
となります。
振幅Vr(p-p)はピーク値Vrpの2倍になるので、
Vr(p-p)=2×Vrp=2√2×Vr(rms)
この式を変形すると、(2)式になります。
コンデンサ容量を求める
リップル率rfのグラフから、求めたrfに該当するパラメータωCRLを求めます。
この時、もう一つのパラメータであるRs/RLについては、Rsが未定なので、
ωCRLは、Rs/RL=0.1~30で求まる範囲になります。
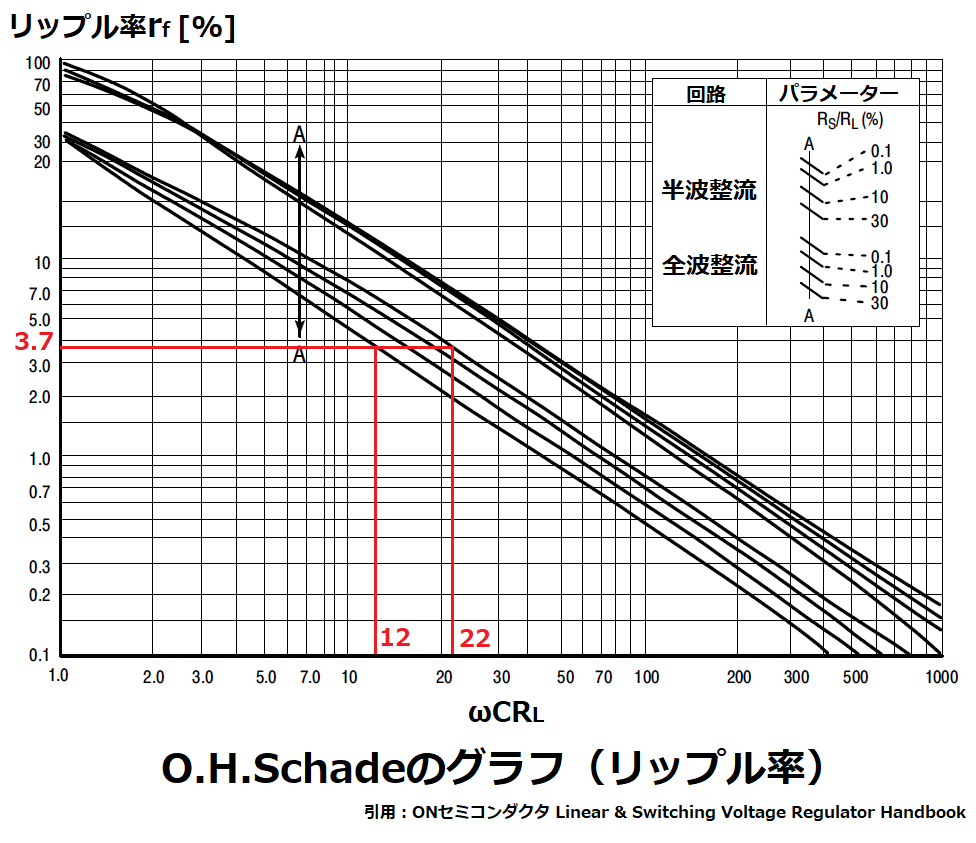
本例の場合、rf=3.7%となるωCRLの範囲は、
ωCRL=12~22
次に出力/入力電圧率のグラフを使用して、
パラメータωCRLとRs/RLを確定させます。
本例の場合、ωCRL=12~22の範囲において、
Vout/Vin=134/141≒0.95=95[%]
となるパラメーターを選定します。
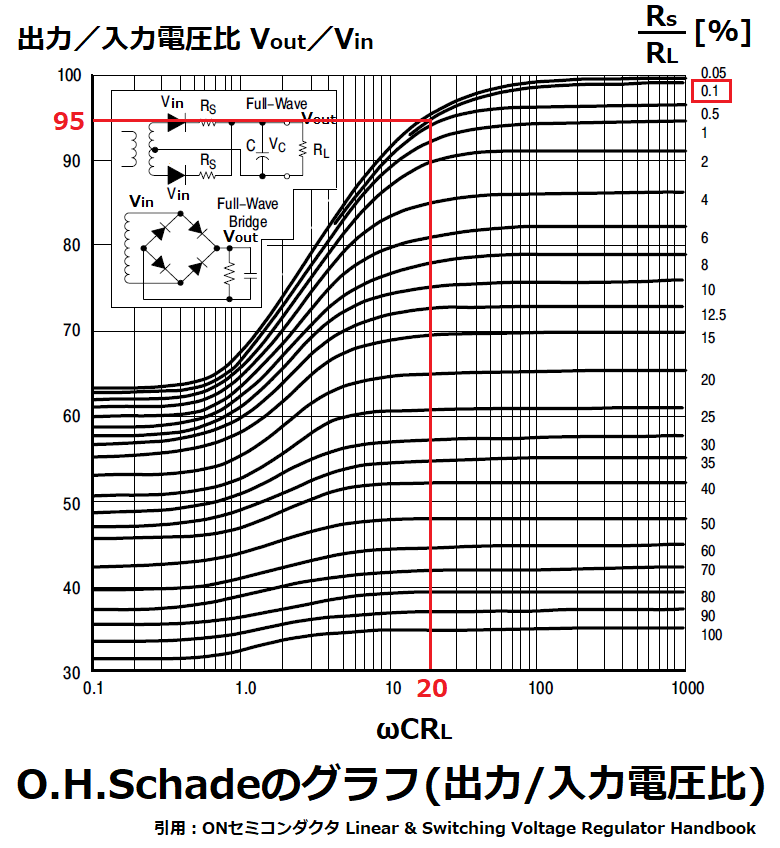
ここで、
Rs/RL=0.1、ωCRL=20
とした場合、リップル率rfのグラフを再び参照すると、
rf=4%
になります。
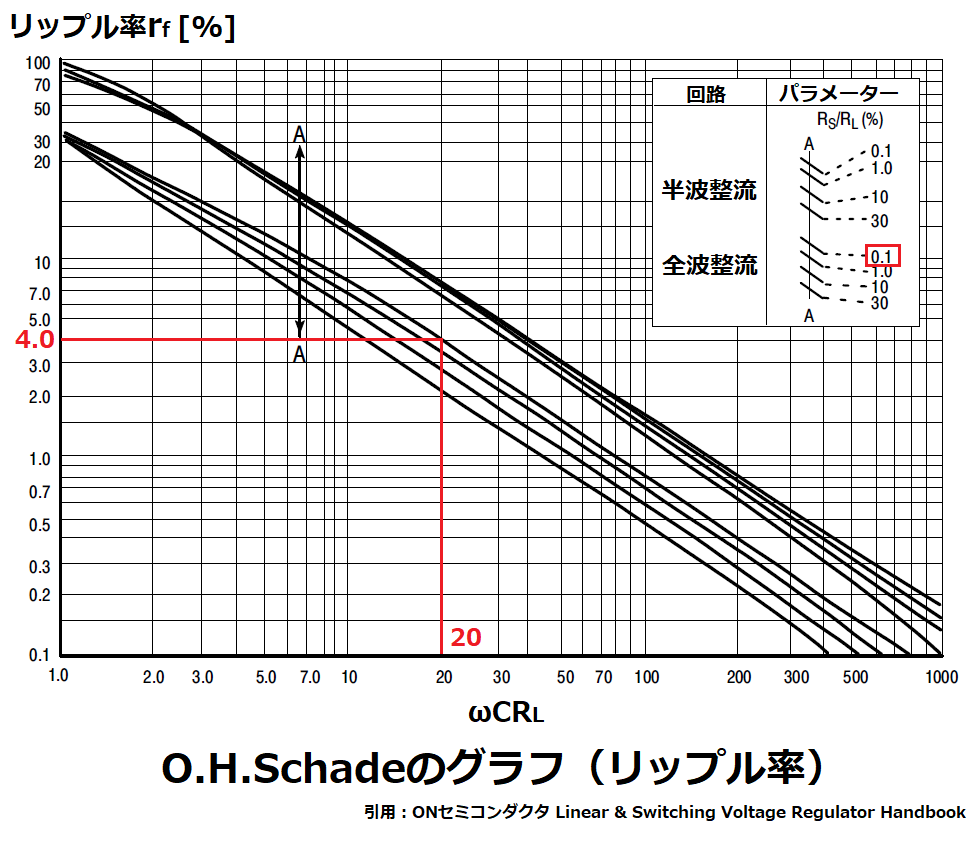
リップル電圧の実効値は
Vr(rms)=rf×Vout
=0.04×134=5.36[V]
リップル電圧の振幅幅Vr(p-p)は、
Vr(p-p)=2√2×Vr(rms)
=2√2×5.36
≒15.2[V]=±7.6[V]
となり、設計目標のリップル幅±7Vよりも少し大きくなりましたが、
実際の値は多少異なってくることから、目安としては十分です。
ωCRL=20より、平滑コンデンサ容量Cは、
C=20/ωRL
=20/(2×π×50×447)
≒142×10-6[F]=142[uF]
電解コンデンサの容量(E12系列)より、
直近の150uFを選定します。
Rsについては、Rs/RL=0.1%、RL=447Ωなので、
Rs=0.001×447=0.447[Ω]
になります。
出力/入力電圧率のグラフから分かるように、
電源からコンデンサ間の抵抗値はRs以下にしないと、
出力電圧が低下することになります。
このため、突入電流防止用に数Ω程度の抵抗を接続する場合は、
通電後の温度上昇により抵抗値が低下するNTCサーミスタや、
起動時のみ抵抗を経由させ、その後はリレーやサイリスタ等で
抵抗間をショートさせる等の方法を取ります。
ダイオード電流を計算する
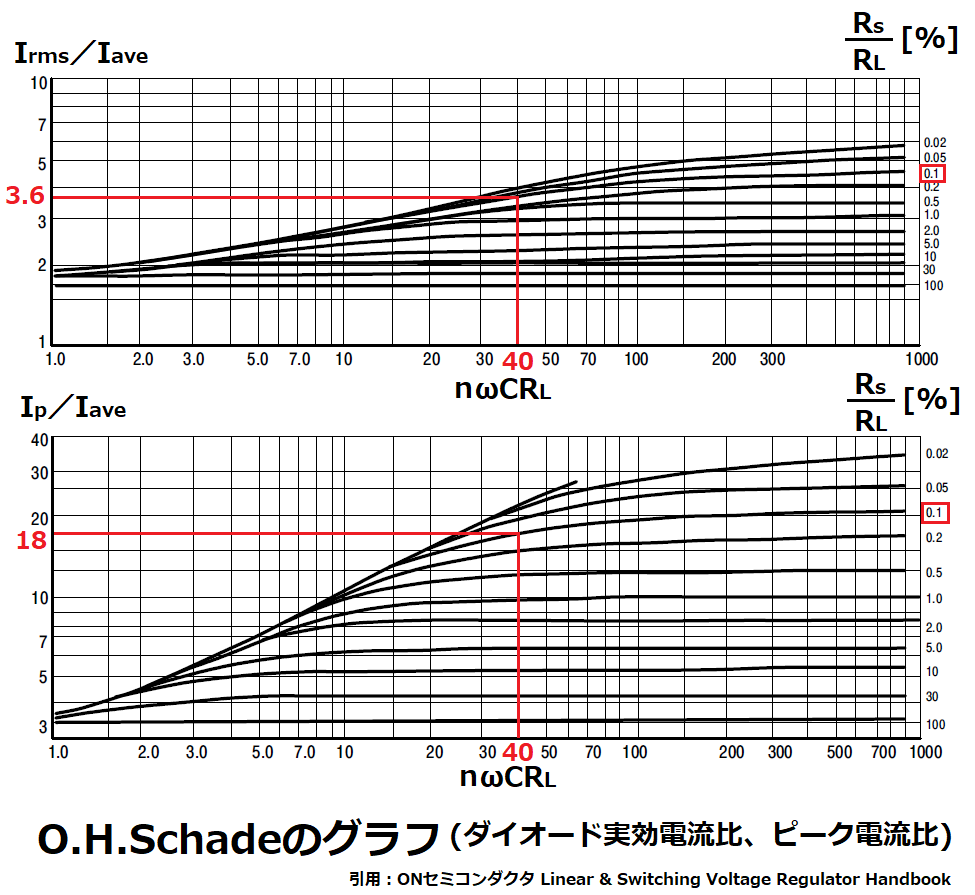
ダイオード実効電流比Irms/Iave、ピーク電流比Ip/Iaveのグラフを用いて、
ダイオードに流れる電流値を求めます。
このグラフの横軸はnωCRLとなっており、
全波整流の場合、n=2となります。
(半波整流の場合は、n=1)
本例の場合、
nωCRL=2×20=40、Rs/RL=0.1
に相当する電流比をグラフから読み取ります。
Irms/Iave=3.6、Ip/Iave=18
ダイオードの平均電流Iaveが整流回路の出力電流Ioutとほぼ同等と考えた場合、
実効電流値は、
Irms=3.6×Iave
=3.6×300[mA]=1080[mA]=1.08[A]
ピーク電流値は、
Ip=18×Iave
=18×300[mA]=5400[mA]=5.4[A]
となります。
コンデンサのリップル電流
電解コンデンサに流れるリップル電流Icr(rms)は以下の式から求めます。
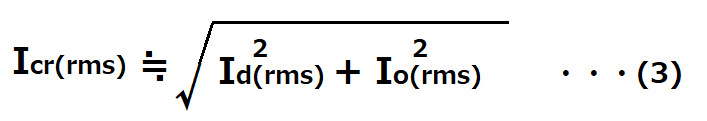
Id(rms):ダイオード実効電流[A]
先程グラフから求めたダイオードの実効電流値になります。
Io(rms):整流回路の出力電流[A]
この値も実効値になります。
本例では抵抗負荷なので、平均電流値と同じですが、
整流回路の後段がスイッチング電源の場合、
トランスの一次側電流の実効値になります。
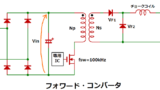
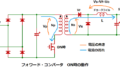
フライバック/フォワード電源の一次側実効電流の求め方については
下記記事で解説しています。
本例の場合、リップル電流は
Icr(rms)=√(Irms2+Iout2)
=√(1.082+0.32)
≒1.12[A]
となります。
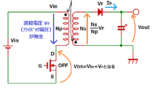
<(3)式になる理由>
下図の様に、コンデンサへの電流icは、
ダイオードからの電流idと、
整流回路の出力電流ioの差になるので、
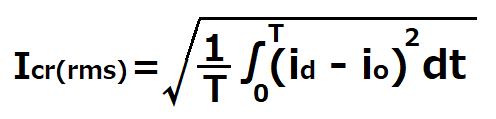
T:入力電源の周期T(本例の場合、50Hzなので20ms)
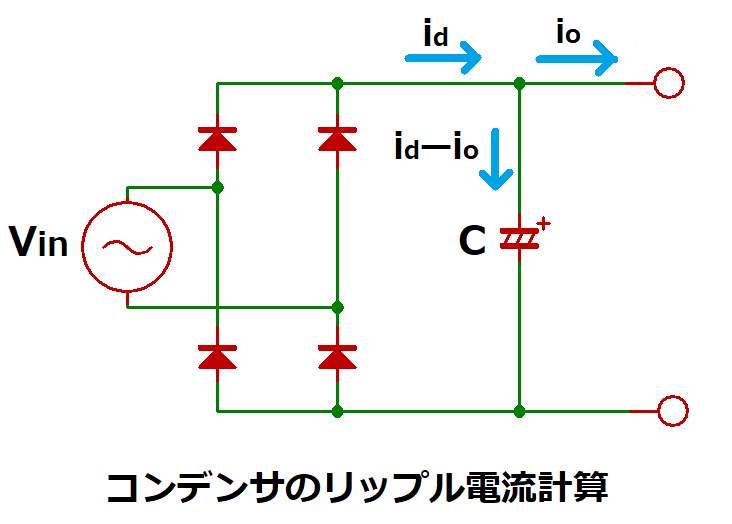
この式を解くのは手間がかかるため、
以下の関係であることを利用して、式を簡略化します。
(id>0、io>0なので、二乗の括弧内を展開したとき、2×id×ic分だけ右辺の方が大きい)
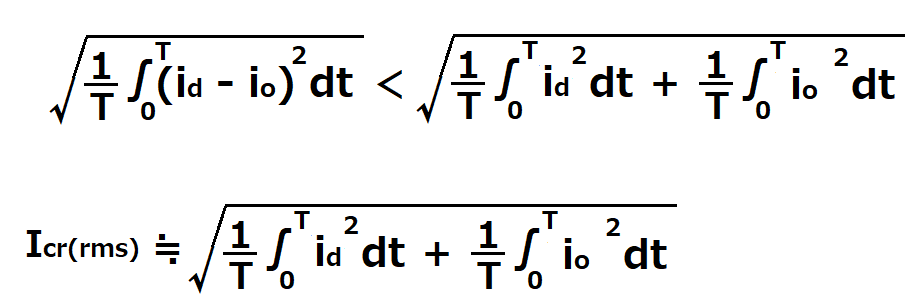
id、ioの実効値を、ぞれぞれId(rms)、Io(rms)とすると
Ic(rms)=√(Id(rms)2+Io(rms)2)
と(3)式になり、リップル電流のおおよその値が求められます。
以上より、グラフを用いた算出結果は次のようになりました。
出力電圧:134V ±7.58V
ダイオード電流:ピーク値5.4A 実効値1.08A 平均値0.3A
リップル電流:実効値1.12A
LTspiceを用いたシミュレーション結果
もう一つの方法であるSPICEを用いて求めた結果が以下になります。
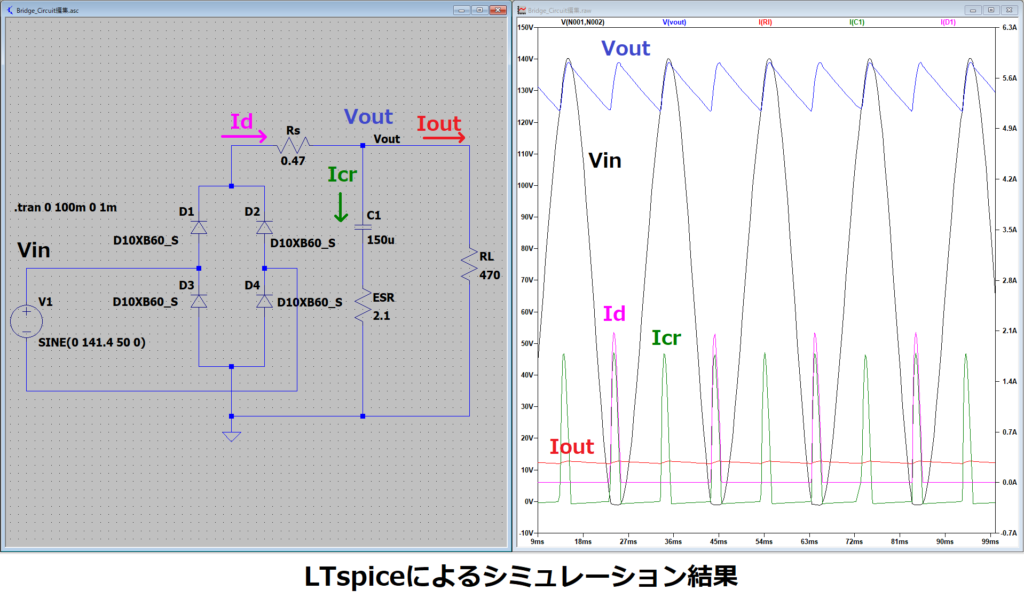
ここでは、グラフで求めたパラメータ(C、RL、Rs)以外に
電解コンデンサのESRを2.1Ω(※1)に設定しています。
※1:ESR(等価直列抵抗)の値については、
コンデンサの誘電損失tanδから次式で求めます。
ESR=tanδ/2πfC
コンデンサのtanδはカタログに記載されており、本例では0.2とした場合、
ESR=0.2/(2×π×100×150×10-6)) ≒2.1Ω
となります。
<シミュレーション結果>
出力電圧:131.5V±7.5V
出力電流:279mA
ダイオード電流:ピーク値2.1A 実効値0.44A 平均値0.12A
リップル電流:0.6A(実効値)
リップ電圧の振幅幅±7.5Vはグラフで求めた値とほぼ一致しました。
出力電圧の差も僅かです。
ダイオード電流、リップル電流については、シミュレーションの方が小さい値となりました。
実測値との比較
今回、算出したコンデンサ容量でブリッジ整流回路を実際に製作し、
電圧、電流値を測定してみました。
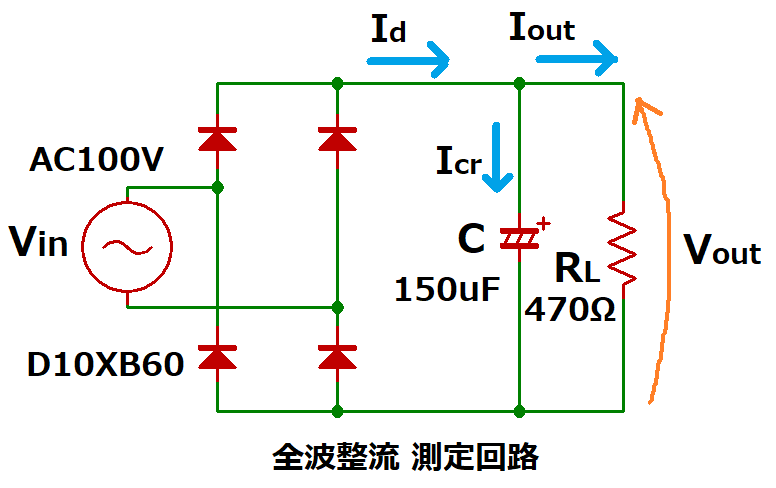
<回路条件>
・入力電圧 AC100V 50Hz(AVR 使用)
・ブリッジダイオード:新電元工業製 D10XB60 (600V 10A)
・負荷抵抗:470Ω(電子負荷 使用)
・平滑コンデンサ: 150uF 200V(日本ケミコン製 KXJシリーズ)
・内部抵抗Rsは0.47Ωと非常に小さいので省略
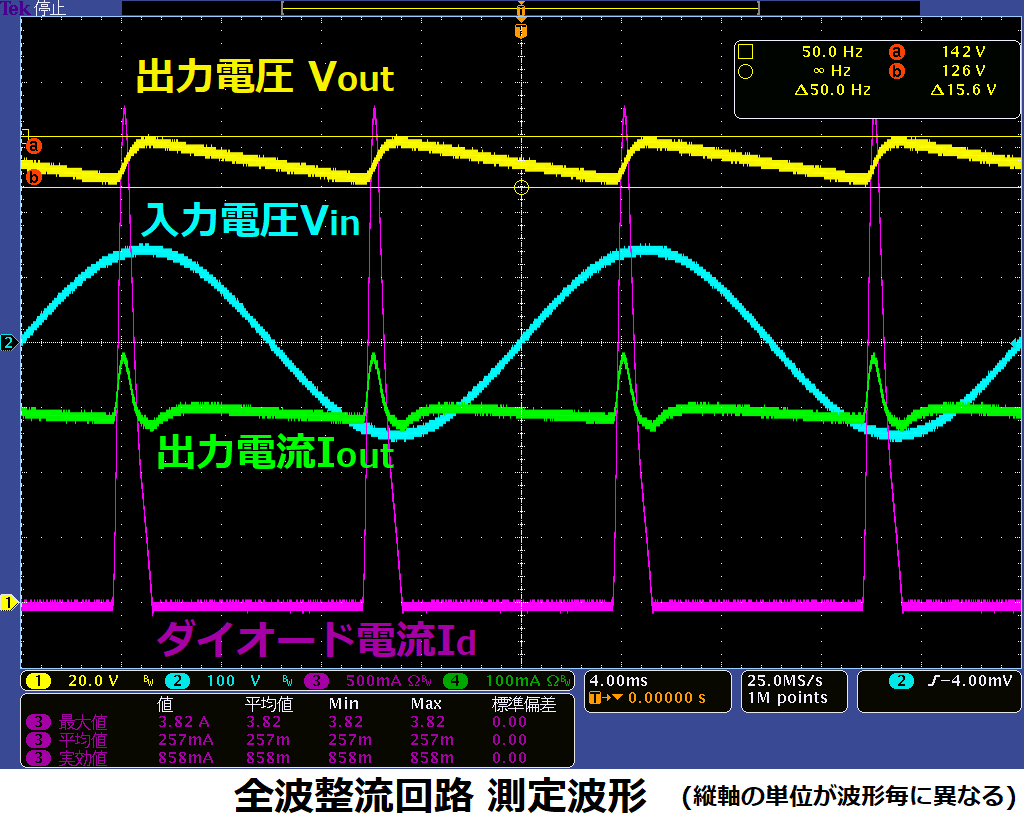
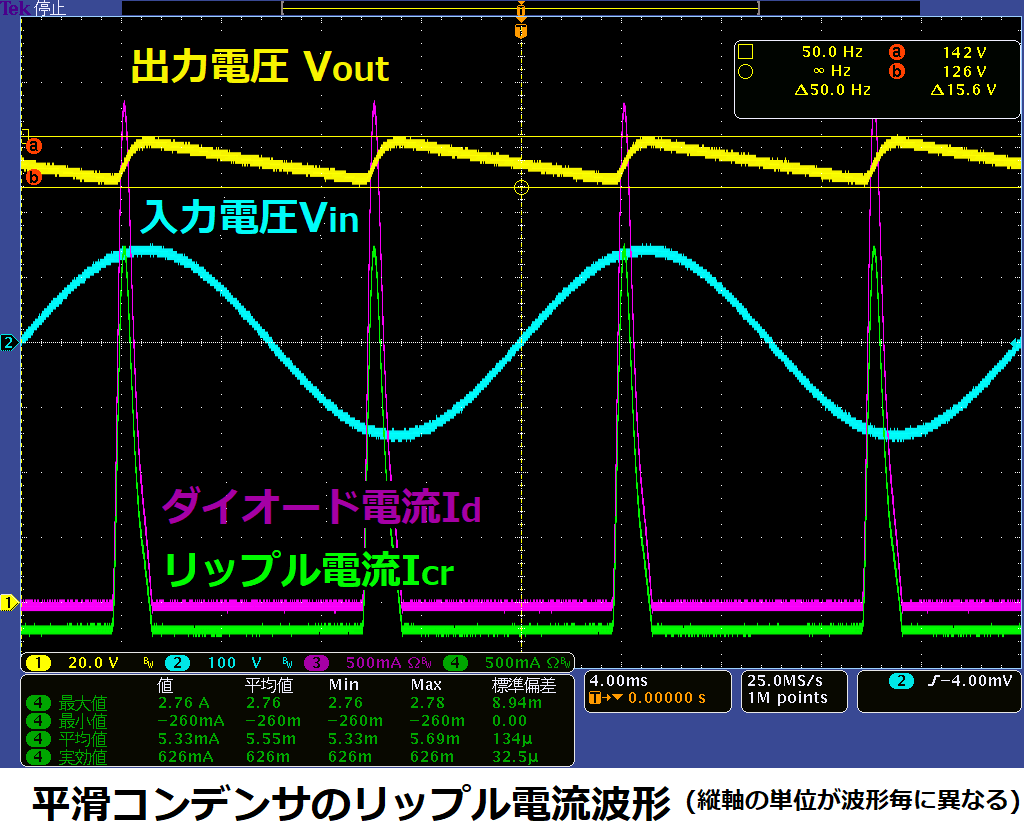
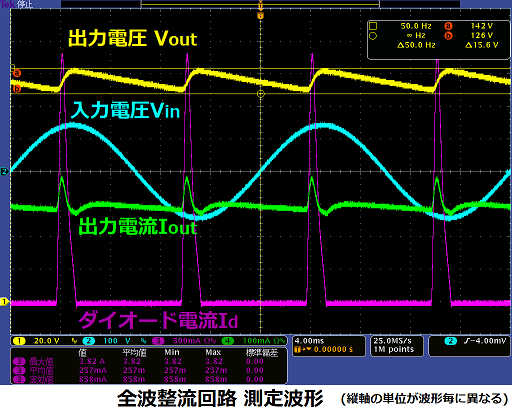
<測定結果>
出力電圧:134V±8V
出力電流:295 mA
ダイオード電流:ピーク値:3.8A 実効値:0.86A 平均値:0.26A
リップル電流:0.63A(実効値)
これまでの結果をまとめると以下になります。
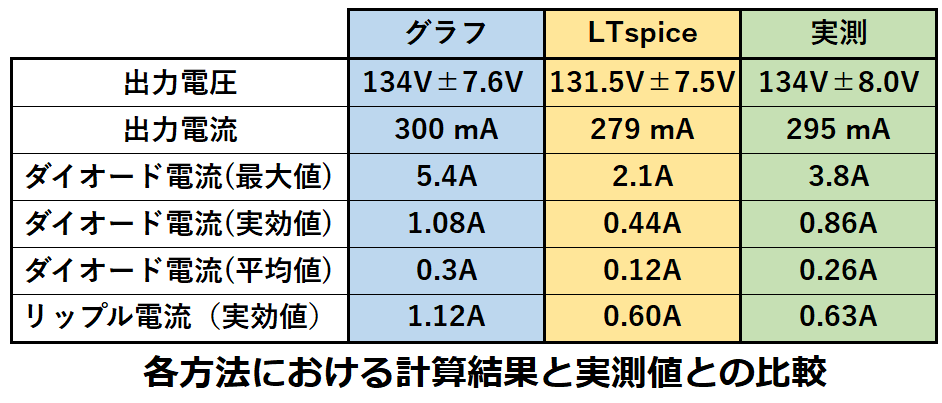
出力電圧は、グラフ及びSPICE共に実測値とほぼ同じとなり、
どちらの方法でも精度が高いと言えます。
ダイオード電流については、実測値に比べ、
グラフは大きく、SPICEは小さくなりました。
リップル電流は、SPICEの精度が高い結果となりました。
この結果から、グラフを用いた場合、電圧値の精度は良いが、
電流値については、参考程度とした方が良いです。
どちらの方法でも、最終的には実際に測定し、
部品の定格に対して十分なディレーティングを確保できているか必要があります。
(電流の場合、定格の80%以内)
★電解コンデンサのリップル電流測定方法について解説しています。
★半田付けのコツや部品の外し方を解説しています。
★試験・工作時で役立つ工具類を紹介しています。