この記事でわかること
・インダクタンスと巻き数の算出法
・ギャップ長、巻線の線径の決め方
・損失と上昇温度の確認方法
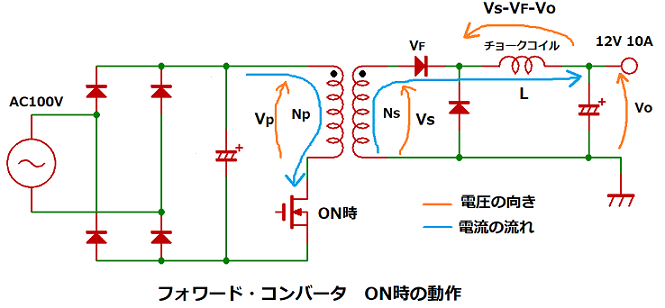
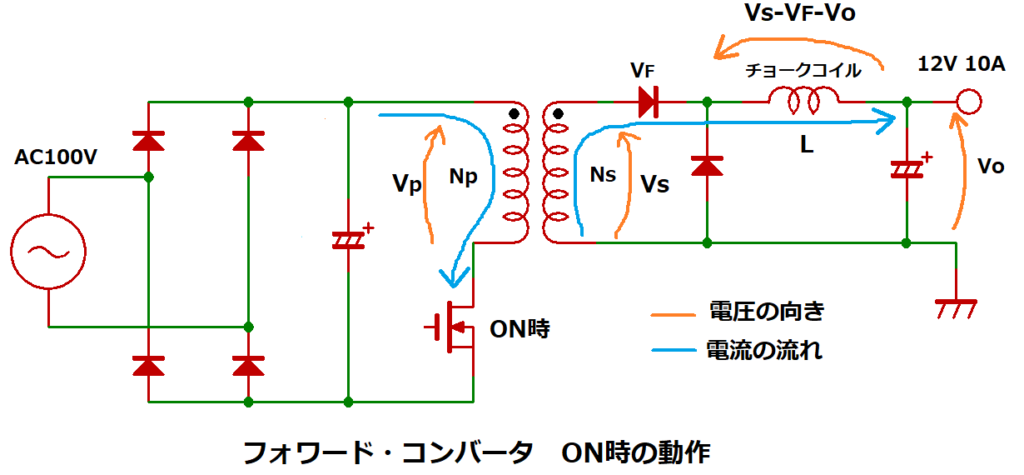
前回、フォワード・コンバータのトランス設計方法を解説しました。
フライバック・コンバータではトランスは電圧変換だけでなく、
エネルギーを蓄えるチョーク・コイルとしての役割も担うのに対し、
フォワード・コンバータの場合、トランスは電圧変換のみを行い、
エネルギーを蓄える役割は二次側に設けるチョーク・コイルが担います。
本記事では、フォワード・コンバータのチョーク・コイル設計方法を説明します。
チョーク・コイル設計手順
以下の順番でチョーク・コイルの各種仕様を決めていきます。
1.インダクタンス
2.巻き数
3.線径
4.銅損
5.温度上昇度
ここでは、前回のトランス設計で解説した
フォワード・コンバータに使用するチョーク・コイルを例にします。
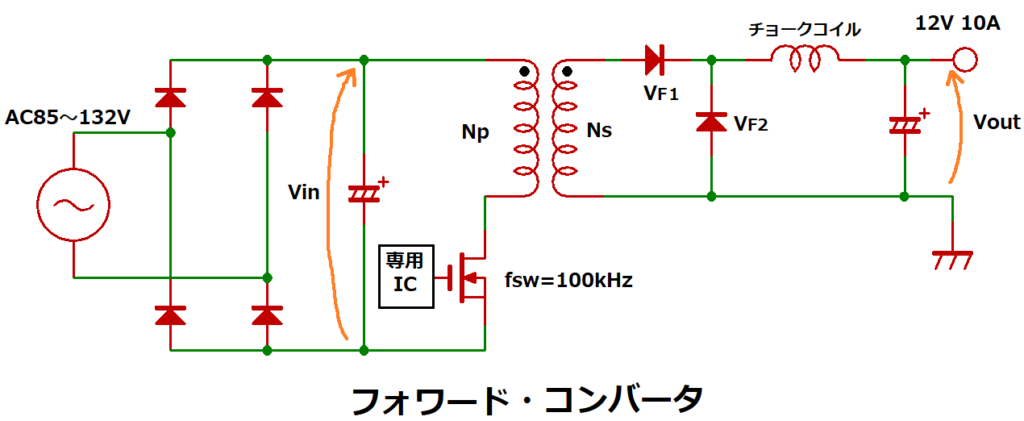
・電源仕様
入力:AC100V(AC85~132V) 50/60Hz
出力:DC12V/10A (120W)
スイッチング周波数:100kHz
・トランス設計時に以下の項目が決定しています。
トランスの巻き数比:38/11
ONデューティー:0.35(定格動作時)
インダクタンスL
インダクタンスは下記式より求めます。
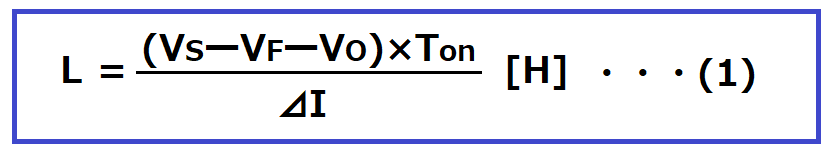
VS:トランスの二次側電圧[V]
VO:出力電圧[V]
VF:整流ダイオードの順方向電圧[V]
Ton:定格動作時のON時間[s]
トランス設計時に設定したONデューティと周波数から算出します。
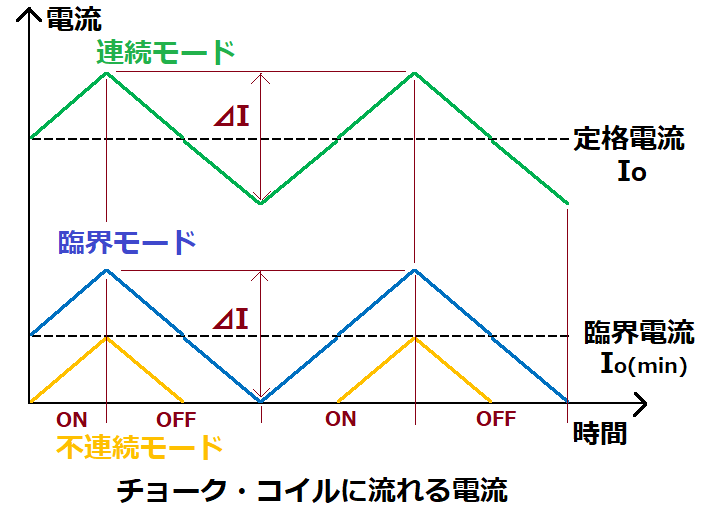
⊿I:チョーク・コイルに流れる電流の変化量[A]
⊿I=Io(min)×2
Io(min):臨界電流 臨界モード時の平均電流(≒0.1×Io)
臨界電流Io(min)を定格電流Ioの10%程度に設定すると、
形状、コスト、制御性において最適になるとされています。
<計算例>
トランスの巻き数比が決まっているので、
一次側電圧Vpから求めます。
定格入力AC100Vの場合の一次側電圧Vpは、
Vp=100×√2×0.9=127V
ここで、0.9を掛けているのは、ブリッジダイオードによる
全波整流回路において、リップルによる電圧降下を10%にした場合を想定しています。
(詳細はトランス設計の記事を参照)
巻き数比Np/Ns=38/11より、二次側電圧Vsは、
Vs=Vp×Ns/Np
=127×11/38≒36.7V
臨界電流Io(min)を定格電流10Aの10%である1Aにすると、電流の変化量⊿Iは
⊿I=Io(min)×2
=1A×2=2A
定格動作時のON時間はONデューティー0.35より、
Ton=D/f
=0.35/100kHz
=0.35×10us=3.5us
整流ダイオードVF1の順方向電圧VFを0.55Vとすると、インダクタンスLは、
L=(VsーVFーVo)×Ton/⊿I
=(36.7―0.55ー12)×3.5×10-6/2
≒42×10-6[H]=42[uH]
<参考:(1)式になる理由>
インダクタンスの公式より
V=L・di/dt
変形して、
L=V・dt/di=V・ton/ΔI
チョークコイルに印加される電圧Vは
(トランス二次側電圧Vsーダイオードの順方向電圧VF)と
出力電圧Voとの電位差になるので、
L=(VsーVFーVo)・ton/ΔI
巻き数N
巻き数はAL値の公式 AL=L/N2 を変形して求めます。

L:インダクタンス [nH]
AL:コア選定に使用するパラメータ 単位は[nH/N2]
コアカタログを見ると、AL値に関する2つのグラフ(AL値-ギャップ、NI(limit)ーAL値)があります。
これは、ギャップを変えるとAL値が変化し、
AL値によって、流せる電流量が決まることを意味します。
電流を多く流すためにはギャップを広くして磁気飽和を防ぐ必要がありますが、
インダクタンスLが減少してしまいます。

このため、コアサイズとギャップについては、何回か試行錯誤して決めることになります。
コアサイズについては、だいたいの目安として、
トランスのコアより一回り小さいサイズを選びます。
そして、まずは、AL値ーNI(limit)グラフから、
ディレーティング20%における中央付近のAL値を選択し、
(2)式より、巻き数Nを計算します。
求めたNと定格電流Iの積がNI(limit)よりも小さいか確認します。
N×I<NI(limit)
ここで、I(limit)は、磁気飽和せずに流せる電流になります。
Ni(limit)よりも値が大きい場合は、
ギャップを増やすか、コアサイズを大きくしてAL値を下げる必要があります。
<計算例>
トランスのコア(EER35)より一回り小さいEER28を選択します。
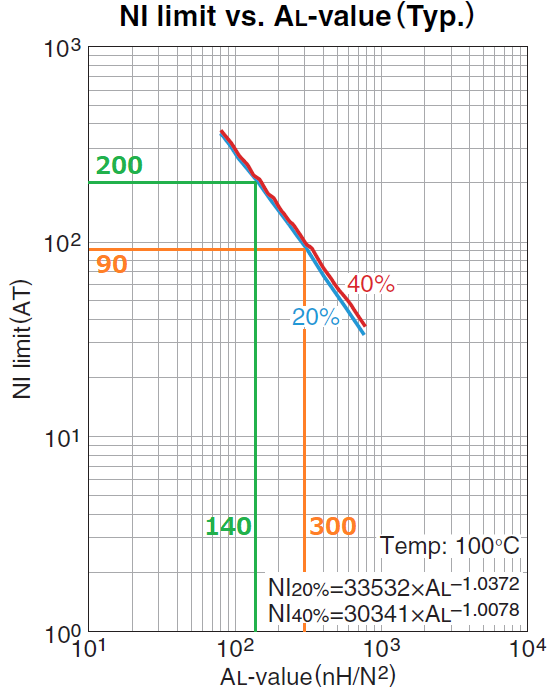
AL値ーNI(limit)グラフの中央値を読み取ると、
AL=300[nH/N2]の時にNI(limit)=90[AT]です。
巻き数Nは、
N=√(L/AL)
=√(42[uH]/300[nH/N2])
≒11.8
なので、12ターンとした場合、
12T×10A=120ATとなり、NI(limit)の90ATを超えてしまいNGとなったので、
ギャップを増やしてみます。
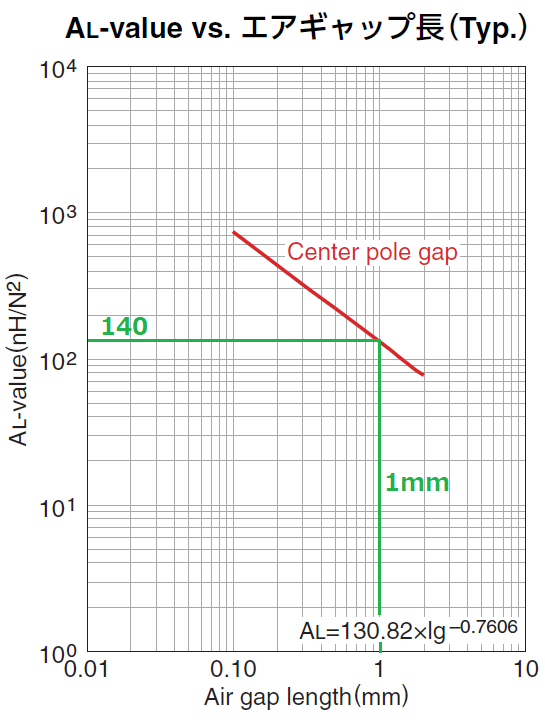
AL値-ギャップ特性グラフより、ギャップを1mmにしてAL値を140[nH/N2]に下げます。
この時のNI(limit)は200ATになります。
巻き数Nは
N=√(L/AL)
=√(42[uH]/140[nH/N2])
≒17.3
なので、18ターンとした場合、
18T×10A=180ATとなり、NI(limit)の200AT以下なのでOKとなります。
線径
巻線の単位面積あたりの許容電流を電流密度(電流容量)と呼びます。
チョーク・コイルに使用されるエナメル線の電流密度は3~5[Arms/mm2]程度です。
この電流密度を目安にして、巻線に必要な線径Φを算出します。

Irms:電流(実効値)[A]
δ:電流密度(3~5[Arms/mm2])
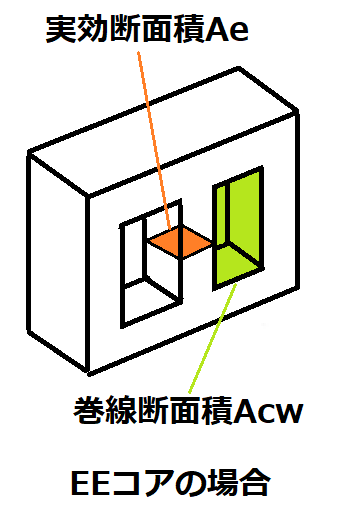
そして、求めた線径の巻線をコアにターン数分、巻くことができるか確認します。
巻線の占める面積(巻線の断面積×ターン数)が、
コアカタログの巻線断面積Acwの50%程度までに収まっていればOKです。
<計算例>
電流密度を5[Arms/mm2]とした場合、必要な線径Φは、
Φ=2×√(Irms/(π・σ))
=2×√(10/(π×5))
≒1.59[mm]
必要な線径が求まりましたが、実際にコアに巻く場合、
Φ0.5より太いと巻き難いので、Φ0.5を並列接続することを考えます。
並列接続時に必要な本数は、
Φ0.5の1本あたりの断面積が0.252×π=0.196mm2なので
巻線に必要な断面積 10[A]/5[Arms/mm2]=2[mm2]より、
2/0.196≒10.1本となります。
しかしながら、3本を超える並列巻きは巻きずらい為、リッツ線を使用します。
リッツ線は、細い素線を撚り合わせて1本にした電線で、
表皮効果の影響を抑えることができることから、
電流密度も6~8[Arms/mm2]程度まで大きくできます。

電流密度を8[Arms/mm2]とした場合、
巻線に必要な断面積Sは、
S=10[A]/8[Arms/mm2]=1.25[mm2]
Φ0.18×60のリッツ線を使用した場合、断面積は
0.092×π×60≒1.53mm2
なので、巻線に必要な断面積1.25より大きいのでOKです。
次に巻線がターン数分、コアに巻けるか検討します。
17ターン巻いた時の巻線が占める面積は
1.53[mm2]×17≒26[mm2]

コアEER28の巻線断面積Acw=114mm2なので、
占有率は
26/114≒23%
と50%以内なので問題ありません。
ここで使用した電流密度は、あくまで目安なので、
実際には試作して、動作時の巻線温度を測定し、
エナメル線の耐熱温度120℃以下になるようにします。
この時、測定時の周囲温度が25℃で、電源仕様の周囲温度上限が60℃としたら、
その温度差35℃を巻線温度測定値に加えても120℃以下にしなくてはなりません。
銅損Pcと上昇温度
チョークの損失はコア損失Pc(鉄損)と巻線の損失Pw(銅損)の合計ですが、
トランスと違い、交流分による鉄損は殆ど無いため無視できます。(※1)
Pm=Pc+Pw≒Pw
巻線の損失Pwは以下の式で求められます。
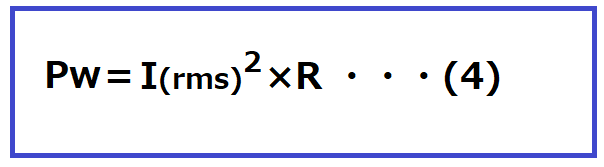
Pw:巻線の損失(銅損)[W]
I(rms):巻線電流の実効値 [A]
R:巻線の抵抗値 [Ω]
巻線の抵抗値Rは次の式から求めます。
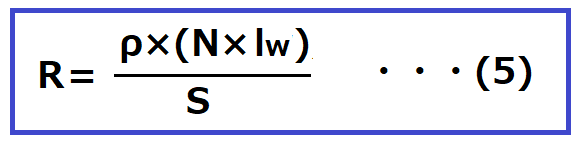
S:巻線の断面積 [mm2]
ρ:銅の抵抗率 [Ω・mm]
ここでは100℃の場合の2.3×10-5[Ω・mm]を使用します。
N:巻線の巻き数 [ターン]
lw:平均巻線長 [mm]
巻線をボビンに1ターン巻いた時の巻線長の平均値です。
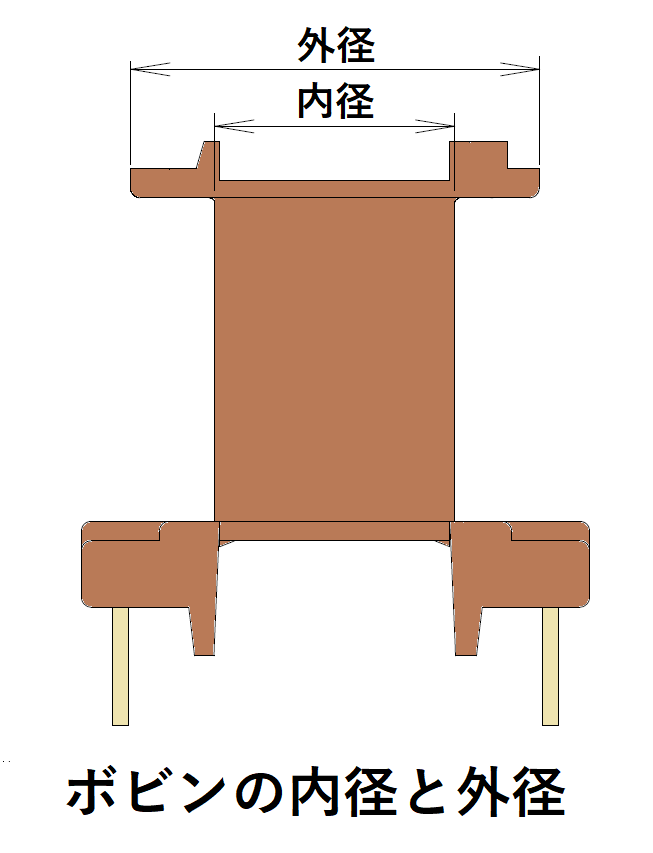
ボビンの内径と外径が判れば、その平均径から、
円周=平均径×πより求めます。
ここでは概算のため、コアの内径と外径の平均値とします。
<計算例>
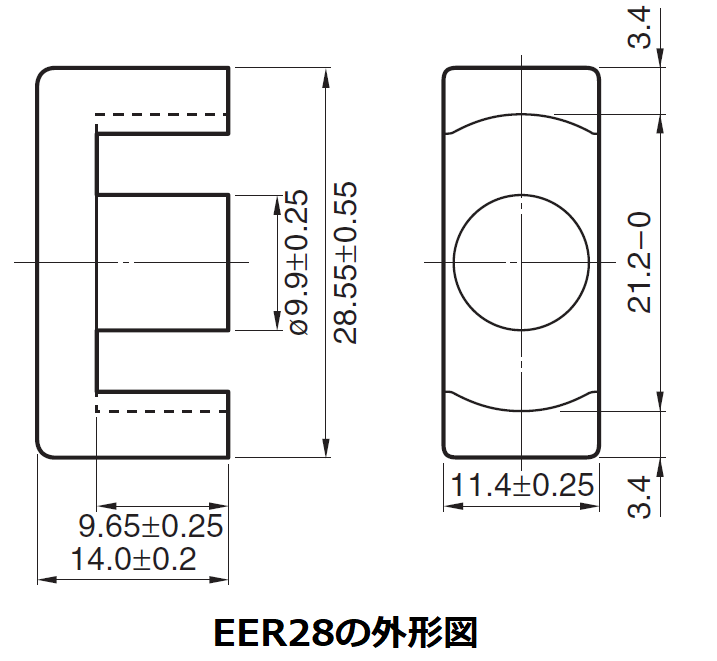
EER28の外形図より、内径9.9mm、外径21.2mmなので、
その平均値15.55mmを用いて、平均巻線長Iwは
Iw=15.55×π≒48.8mm
巻線の抵抗値Rは、
R=ρ×(N×lw)/S
=2.3×10-5[Ω・mm]×17×48.8[mm]/1.53[mm2]
≒1250×10-5[Ω]
よって、巻線の損失Pwは
Pw=I(rms)2×R
=102×1250×10-5=1.25W
チョークコイルの鉄損Pcは無視できるので、
トータルロスPm≒Pc=1.25Wとなります。
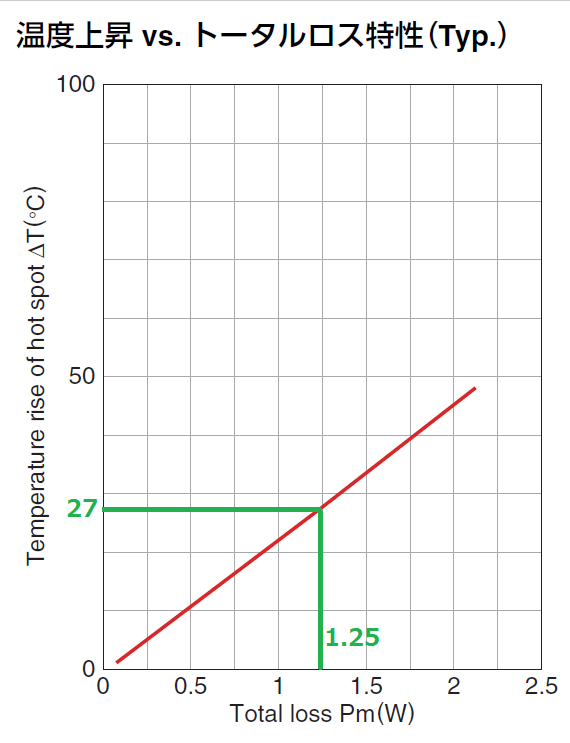
コアカタログ記載の温度上昇ートータルロス特性グラフより、
損失Pm=1.25W時の温度上昇は27℃程度になります。
※1:チョークコイルの鉄損が無視できる理由
コア損失(鉄損)Pcは次の式で求まります。
Pc [kW]=(1/2)×Pcv×Ve・・・(6)
Pcv:単位体積あたりのコア損失[kW/m3]
Ve:コアの実効体積[m3]
Pcvはコア材カタログに記載されているBmーPcvグラフから求めます。
Bmは最大磁束密度ですが、直流しか流れないチョーク・コイルの場合、
磁束密度の変化量ΔBに相当し、以下の式で求まります。
ΔB=V×Ton/(Ae×N) ・・・(7)
=(VsーVFーVo)×Ton/(N×Ae)
Ae:コアの実効断面積
今回の計算例に適用した場合、
ΔB=(36.7―0.55ー12)×3.5us/(17×82.1×10-6m2)
≒0.060[T]=60[mT]
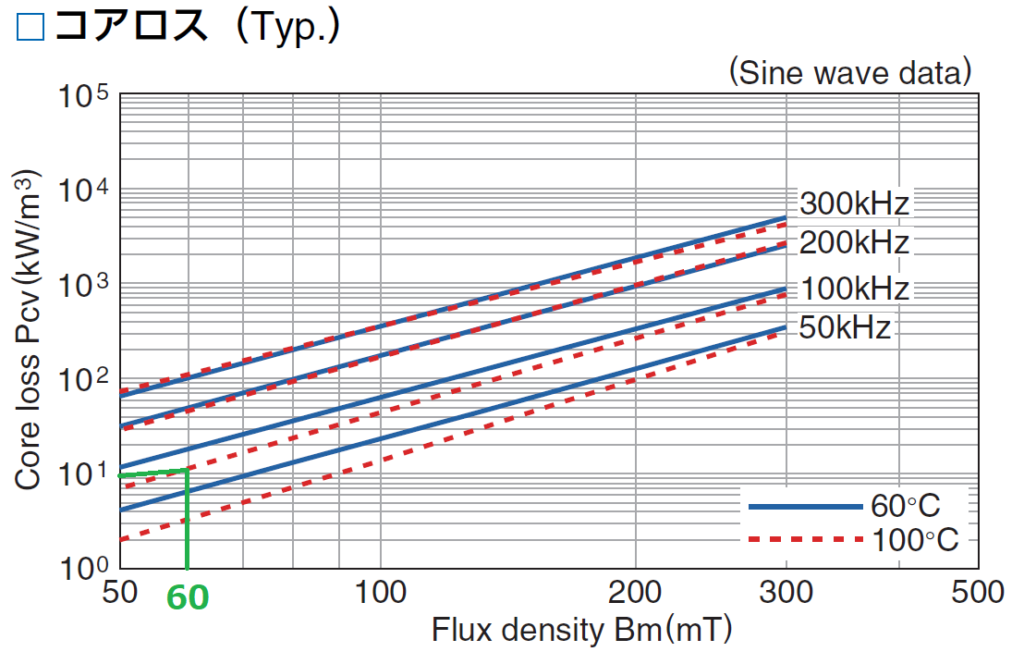
グラフよりPcv≒10[kW/m3]程度となります。
コアの実効体積Veはコアカタログより、
5250[mm3]=5250×10-9[m3]なので、
鉄損Pcは
Pc=Ve × Pcv
=5250×10-9[m3]×10[kW/m3]=0.0525[W]
このようにチョークコイルの鉄損は、銅損に比べ無視できる程小さいです。
(※(6)、(7)式になる理由はフォワード電源のトランス設計の記事を参照)
★トランスの作り方について解説しています。
★試作時で役立つ工具類を紹介しています。