この記事でわかること
・ヒートシンクの選び方がわかる
・グリスで温度がどれだけ低下するか
・絶縁シートの使い方と温度への影響
トランジスタやダイオードを使用する時、
消費電力や周囲温度の条件によっては、
ヒートシンクが必要になります。
本記事では、ヒートシンクが必要かどうかの判断基準と、
使用する際の選び方について説明します。
また、必要に応じて、
シリコングリスや、絶縁シートを使用する為、
その使い方と、温度への影響についても解説します。
ヒートシンク選定の手順
ヒートシンクを適用するかの判断と、その選定は次の手順で行います。
①半導体の消費電力を求める
半導体に流れる電圧・電流波形を測定し、
その値から消費電力を計算します。
②半導体の内部温度を算出する
消費電力から、半導体の内部温度(チャネル温度)が求まるので、
最大温度定格を超えないか確認します。
これによって、ヒートシンクが必要かどうか決まります。
③ヒートシンクに求められる熱抵抗値を計算する
温度定格を超えない為に、ヒートシンクの熱抵抗を
どれだけ小さくすれば良いか計算し、
求めた熱抵抗値より小さいヒートシンクを選定します。
④必要に応じてグリスや絶縁シートを選定する
消費電力が大きい場合、
半導体とヒートシンクとの接触部分の熱抵抗の影響も無視できない為、
シリコングリス等で熱抵抗を低減させます。

また、パッケージがフルモールドタイプでない場合、
ヒートシンクも通電される事から、絶縁する必要がある時は、
絶縁シートを間に挟みます。

半導体の消費電力の求め方
・MOSFETの場合
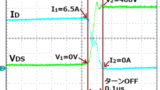
ドレイン・ソース間電圧VDSとドレイン電流ID波形を測定して求めます。
求め方については、下記記事を参照下さい。
下記記事では「損失」という表現をしていますが、消費電力と同じ意味です。
本ブログでは、2つの用語を次のようなイメージで使い分けています。
損失:半導体の内部ロスという観点で、ゲート調整等により減らしたいという場合
消費電力:半導体を製品という観点で、安全動作に必要な条件等を検討する場合
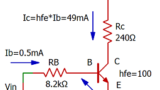
・バイポーラトランジスタの場合
コレクタ・エミッタ間電圧VCEとコレクタ電流ID波形を測定して求めます。
基本的にはMOSFETと同様の方法で求まります。
但し、ON区間の消費電力は、FETではRon × ID2ですが、
トランジスタは、データーシートのコレクタ・エミッタ間飽和電圧VCE(sat)より、
VCE(sat)×IC から求めます。
・ダイオードの場合
オシロスコープの計測機能を用いて、
電流波形の平均値Iaveを求めます。
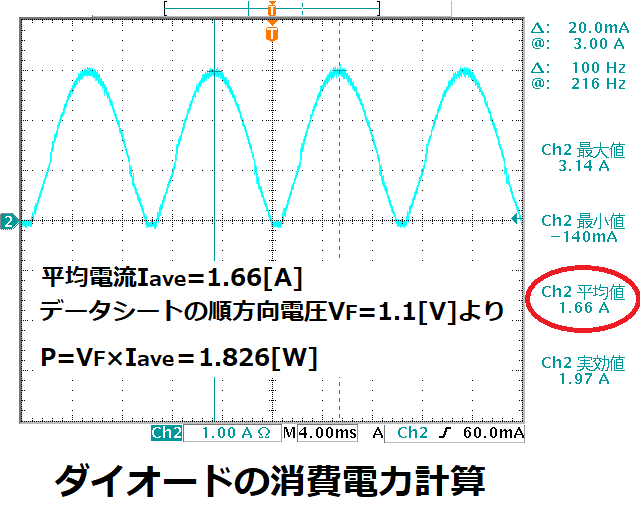
データーシートの順方向電圧VFより、
P=VF × Iave
で求まります。
但し、ブリッジダイオードの場合は、
ダイオードを2つ経由するので、
P=2 × VF × Iave
となります。
半導体の温度計算(放熱器無)
半導体の消費電力が算出できたら、
ヒートシンク無しの場合、
半導体の温度(チャネル温度)が何℃になるか計算します。
例として、東芝製FET TK9A60Dにおいて、
測定の結果、消費電力が2Wであった場合について、
チャネル温度を計算します。
データシートを見ると、
チャネル・外気間熱抵抗Rth(ch-a)が記載されています。
Rth(ch-a)=62.5[℃/W]
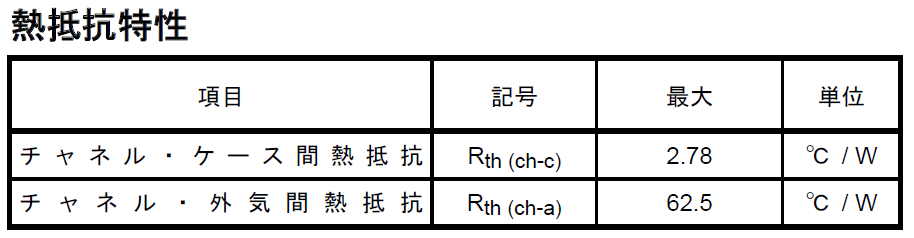
これは、半導体内部と、周囲の空気との間の熱抵抗になります。
抵抗と言っても、単位は[Ω]ではなく、[℃/W]です。
これは消費電力が1Wの時、温度が何℃上昇するかを意味しています。
つまり、消費電力P[W]の時の温度上昇度ΔT[℃]は、
ΔT[℃]=Rth(ch-a)[℃/W] ×P[W]
になります。
これを熱等価回路(熱の流れを電気回路の様に表した図)で表現すると以下になります。
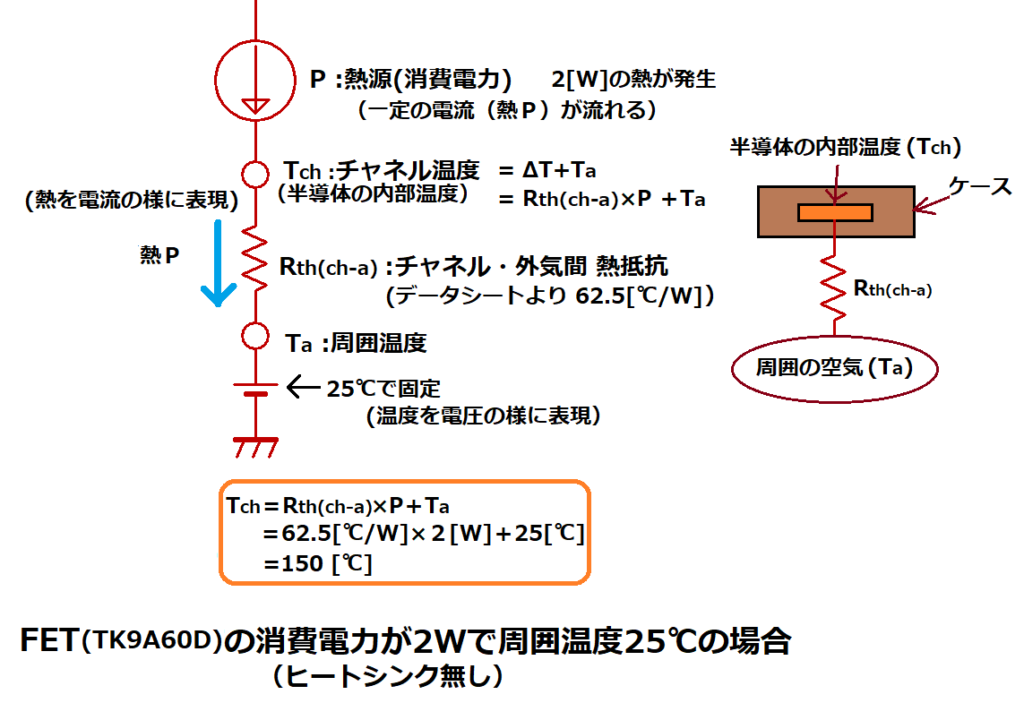
チャネル温度Tchと、周囲温度Taは以下の関係となります。
Tch=ΔT+Ta
=Rth(ch-a) × P+Ta
消費電力P=2[W]、周囲温度Ta=25℃の時、チャネル温度Tchは、
Tch=62.5[℃/W] × 2[W]+25[℃]
=150[℃]
となり、チャネル温度の最大定格は150℃なので、
これ以上、消費電力が大きくなるか、周囲温度が高いとFETが壊れます。
(サイリスタやトライアックの最大定格は125℃が多いので注意)
このため、熱抵抗を小さくして、温度上昇度ΔTを低くする必要があります。
ヒートシンクを付けることで、この熱抵抗を小さくできます。
半導体の温度計算(放熱器有)
ヒートシンクをつける場合は、データーシートにあるもう一つの熱抵抗
チャネル・ケース間熱抵抗Rth(ch-c)を使用します。
Rth(ch-c)は半導体内部と、ケース表面との間の熱抵抗です。
TK9A60Dの場合、
Rth(ch-c)=2.78[℃/W]
であり、先程のチャネル・外気間熱抵抗Rth(ch-a)=62.5[℃/W]に比べ、非常に小さいです。
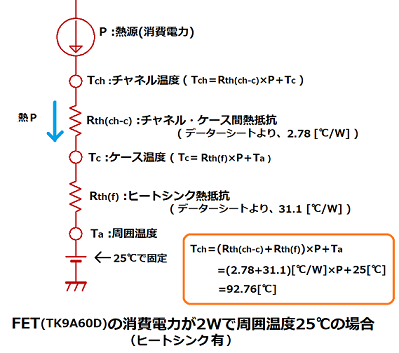
この時の熱等価回路は次の様になります。
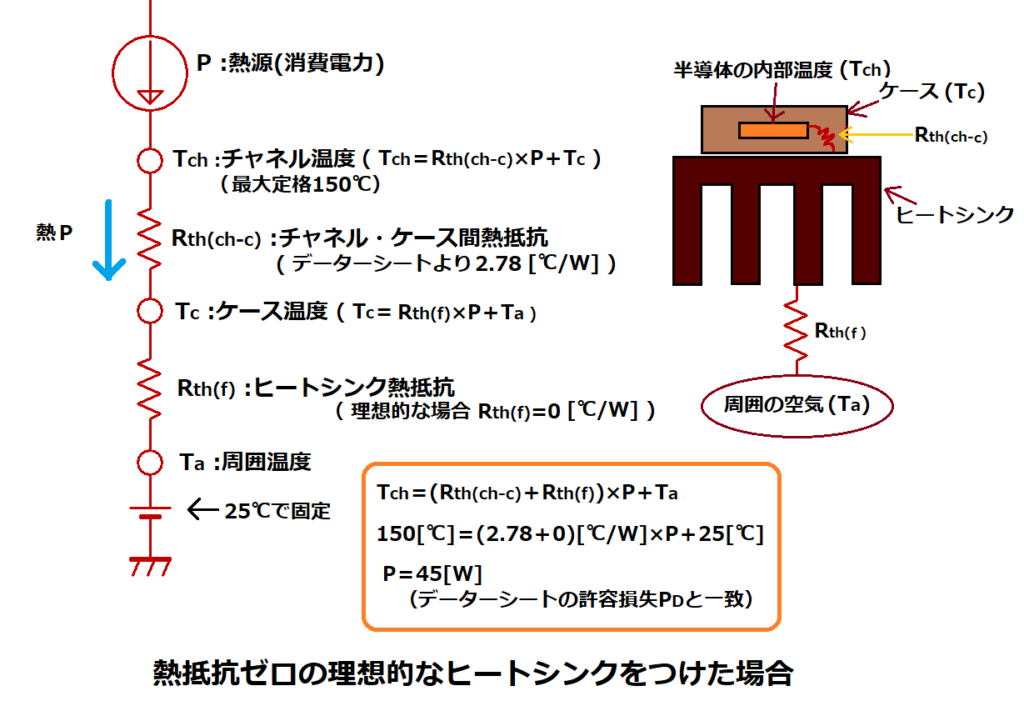
ケース温度をTcとした時、チャネル温度Tchは以下の式で求まります。
Tch=Rth(ch-c) × P+Tc (1)
熱抵抗Rth(f) のヒートシンクを用いた場合、
ケース温度Tcは以下の式で表現できます。
Tc=Rth(f) × P+Ta (2)
(1)、(2)式を組合せることで、
ヒートシンク使用時のチャネル温度Tchは以下となります。
Tch=( Rth(ch-c)+Rth(f) )×P+Ta (3)
ここで、熱抵抗Rth(f)=0の理想的なヒートシンクがあって、
ケース温度Tcを周囲温度Taと同じまで冷やすことが出来たとします。
この時、周囲温度Ta=25℃で動作可能な最大電力Pは
(3)式に、Rth(f)=0、Ta=Tcを代入すると、
Tch=Rth(ch-c) × P+Tc
チャネル温度Tchの最大定格は150℃なので、
150[℃]=2.78[℃/W] × P+25[℃]
P=45[W]
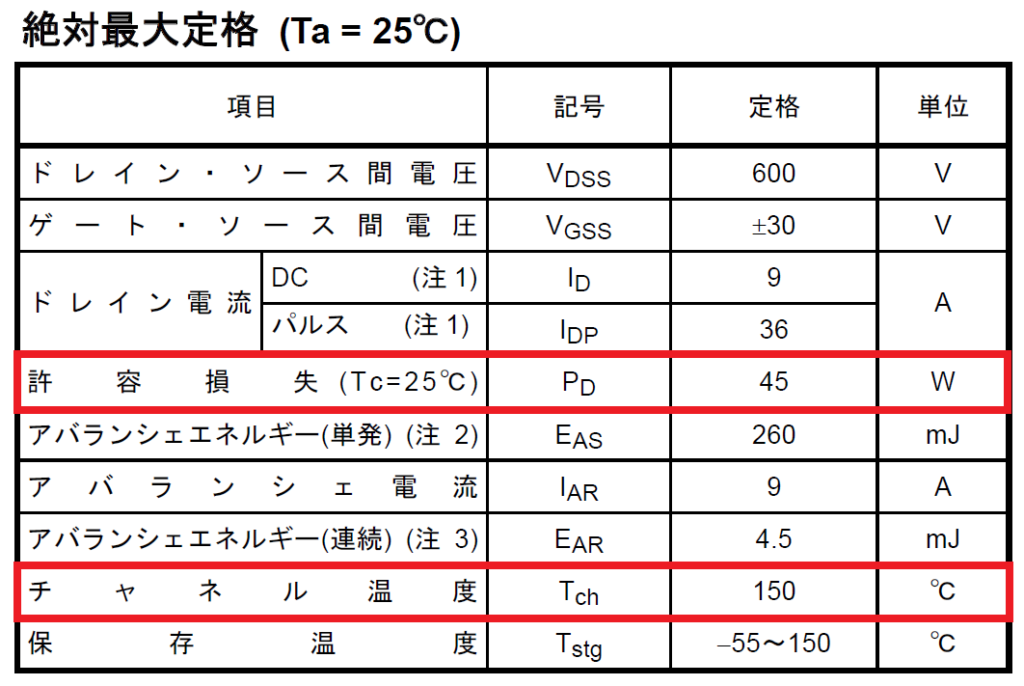
となり、データシート記載の、Tc=25℃時の許容損失(消費電力)PDと一致します。
次に、実際のヒートシンクを用いた場合、
チャネル温度が何℃になるか計算してみます。
条件は先程のヒートシンク無と同様、
消費電力2W、周囲温度25℃で動作した場合です。
ヒートシンクは以下を使用します。
丸三電機製 11PAE15-25B

ヒートシンクの熱抵抗値はデータシートより
Rth(f)=31.1[℃/W]
(データシートでは単位が[K/W]と絶対温度(ケルビン)で表記されていますが、同じです)
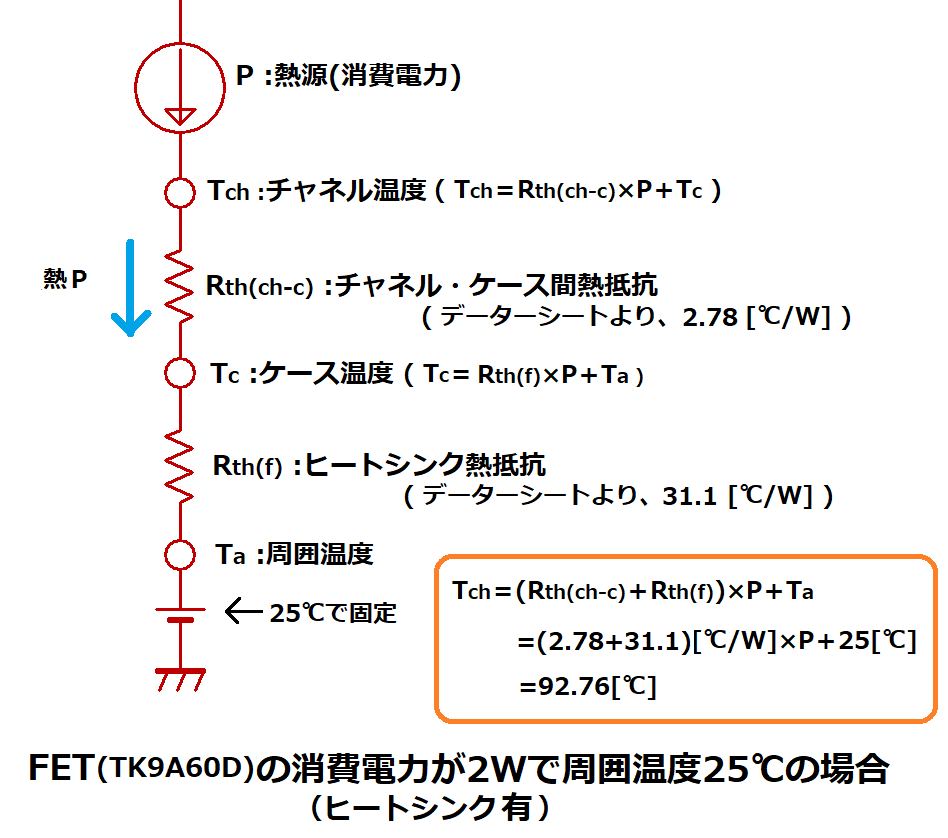
チャネル温度は、(3)式から、
Tch=( Rth(ch-c)+Rth(f) )×P+Ta
=(2.78+31.1)[℃/W] × 2[W]+25[℃]
=92.76[℃]
となり、
ヒートシンク無では150℃もあったチャネル温度を大きく低減させる事ができました。
実際には、ヒートシンクとケースとの接触部分にも熱抵抗が存在するので、
チャネル温度はこれよりも高くなります。
この接触部分の熱抵抗を少しでも小さくする為に、
シリコングリスを接触面に塗布する事もあります。
また、半導体のパッケージによっては、
ヒートシンクと絶縁する必要が生じる場合もあり、
その際は、絶縁シートを間に挟みます。
シリコングリス熱抵抗の求め方
グリスを塗布する半導体パッケージがTO-220の場合で説明します。
使用するグリスは、サンハヤト製SCH-20です。

グリスの仕様を見ると、熱抵抗では無く、熱伝導率[W/m・K]で記載されています。
K=0.84[W/m・K]
これを下記式により、熱抵抗に変換します。
Rth(c-f)=t/(K×L×W)
Rth(c-f) :シリコングリスの熱抵抗[K/W](=[℃/W])
t ∶ シリコングリスの厚み [m]
K ∶ 熱伝導率 [W/m・K]
L ∶ ケース接触面の長さ [m]
W ∶ ケース接触面の幅[m]
TO-220パッケージの長さと幅は
L=15[mm]=0.015[m]
W=10[mm]=0.01[m]
シリコン塗布時の厚み
t=0.1[mm]=0.0001[m]
とすると、
Rth(c-f)=t/(K×L×W)
=0.0001[m]/(0.84[W/m・K] × 0.015[m]×0.01[m])
≒0.8[K/W](=[℃/W])
熱抵抗としては、かなり小さい値となりましたが、
塗布しない場合と比較しないと、どの程度の効果があるのか分かりません。
そこで、グリスの有無による温度への影響について実験を行いました。
グリスの有無による熱抵抗の違い
シリコングリスが実際にどの程度の効果があるか温度測定しました。
<条件>
ダイオード:新電元工業製 SG20SC9M
(TO-220パッケージ)
ヒートシンク:丸三電機製 11PAE15-25B
(熱抵抗:31.1[℃/W])
シリコングリス サンハヤト製 SCH-20
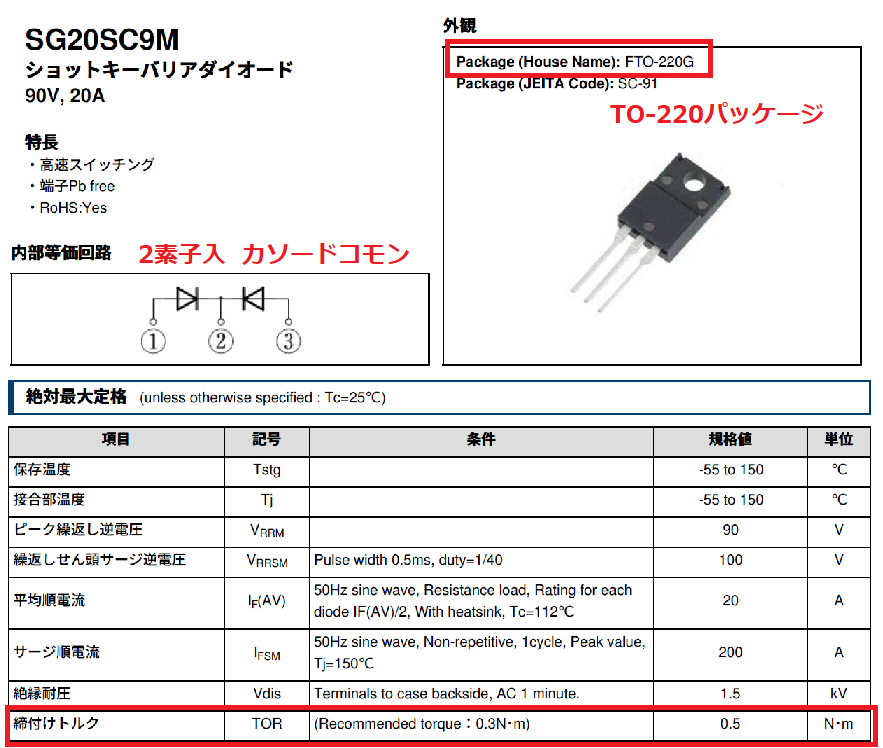
ダイオードをヒートシンクにネジ締めする際の締付けトルクは、
SG20SC9Mのデータシートより0.5[N・m]なので、
この値になるようにトルクドライバを用いて締め付けました。
ダイオードには一定の電流4Aを流しました。
※SG20SC9Mは2素子入り(カソードコモン)ですが、今回は1素子だけ使用
順方向電圧VFの実測値は0.487Vでした。
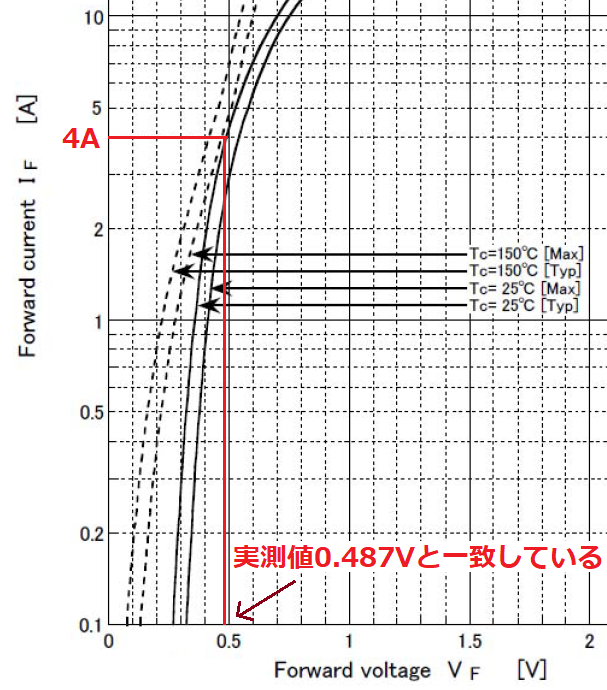
これはデータシートのVF-IF特性グラフとも一致します。
従って、ダイオードの消費電力Pは、
P=VF×IF=0.487[V] × 4[A]≒1.95[W]
になります。
この条件でグリス無しと、グリス塗布した場合の結果は以下になりました。
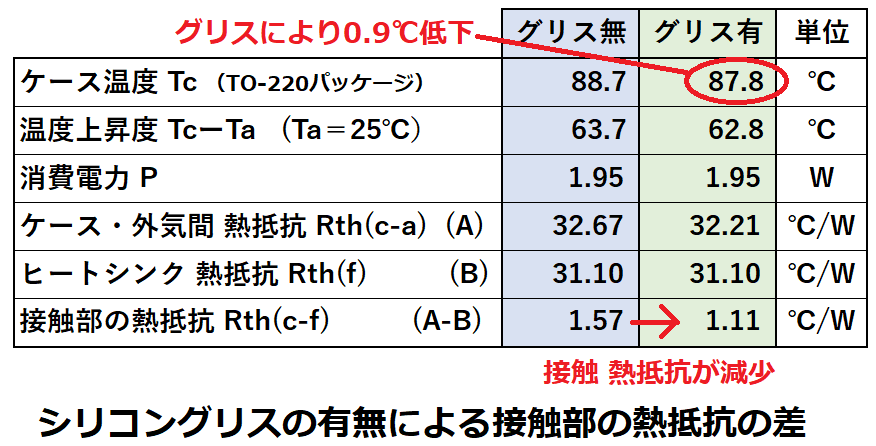
グリスによって、ケース温度Tcが0.9℃低下しています。
このケース温度Tcと消費電力Pから、
ケースとヒートシンク間の接触部の熱抵抗を、
グリス有無それぞれ場合について計算してみました。
(2)式
Tc=Rth(f) × P+Ta
について、ケースとヒートシンク間の接触部の熱抵抗Rth(c-f)を加えると、
Tc=( Rth(f)+ Rth(c-f))× P+Ta
になります。
この式の、Tc、Rth(f)、P、Taの値は分かっているので、
Rth(c-f)を求める事ができます。
その結果、接触部の熱抵抗Rth(c-f)は、
グリス無 1.57[℃/W]
グリス有 1.11[℃/W]
となりました。
グリス有については、先程の計算値0.8[℃/W]より大きくなりましたが、
この計算値はグリス厚0.1mmで均一に塗布されている事が条件となります。
このため、塗布したグリスが厚かった事が、
熱抵抗が大きくなった原因と考えられます。
それでも、グリス無の熱抵抗よりも小さくなりましたが、
消費電力が2W以下と小さかった為、
グリスによる温度低減の効果があまり出ませんでした。
しかし、IPMのような大きなパッケージで大電力を扱う場合は、
接触部の熱抵抗による温度上昇は大きくなる為、グリス塗布は必要になります。
絶縁シートの使い方
絶縁シートは、次のような場合において使用されます。
①半導体とヒートシンク間を絶縁する必要がある場合
半導体のパッケージには、
パッケージ全体が樹脂で覆われているフルモールドタイプと、
ネジ穴の部分(タブ)と裏面が金属になっている金属タブ付きタイプがあります。

金属タブ付きタイプは、金属部分がリードのどれかと導通しています。
トランジスタの場合:コレクタ端子
FETの場合:ドレイン端子
このため、ヒートシンクを絶縁する必要がある場合は、
絶縁シートを挟む必要があります。
何故、このようなパッケージにしているのかと言うと、
熱抵抗を小さくできる為です。
例として、タイプ違いの2つのFETを以下に示します。
TK16A60W(フルモールドタイプ )
Rth(ch-c)=3.13[℃/W] Rth(ch-a)=62.5[℃/W]
TK16E60W(金属タブ付きタイプ)
Rth(ch-c)=0.962[℃/W] Rth(ch-a)=83.3[℃/W]
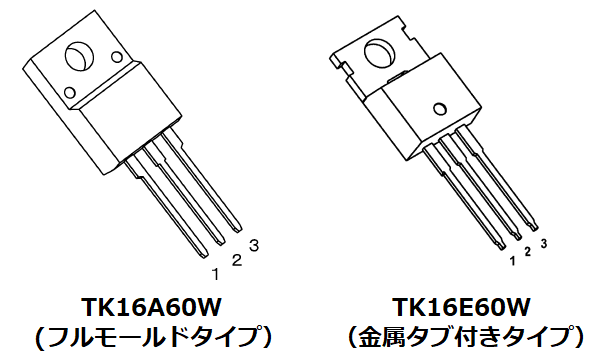
この2つのFETは共にTO-220パッケージで、
最大定格VDS=600V、ID=15.8Aであり、オン抵抗も同じ(Ron=0.19Ω)です。
チャネル・ケース間の熱抵抗Rth(ch-c)を見ると、
金属タブ付きが、フルモールドの1/3以下と非常に小さいです。
このため、許容損失PDに大きな差が出ています。
フルモールド(TK16A60W) PD=40W
金属タブ付き(TK16E60W) PD=130W
従って、金属タブ付きの方が大きな電力を制御できます。
但し、周囲温度間の熱抵抗Rth(ch-a)は金属タブ付きの方が大きくなる為、
ヒートシンクが無い場合はフルモールドの方が適しています。
②半導体と周辺部品との絶縁距離を確保したい場合
フルモールド品でも図のような絶縁キャップやチューブを被せる場合があります。

これは、半導体のリードからヒートシンクまでの絶縁距離を確保したい場合に使用します。
ヒートシンクが筐体(FG)と接続されている場合、
安全規格に適合させるため、一次側回路の半導体にキャップを被せる事で、
半導体のリードとヒートシンク間の空間距離や沿面距離を広げる事ができます。
絶縁距離の求め方については下記で解説しています。
絶縁シートの熱抵抗の求め方
富士高分子工業製 絶縁シート30T-TO-220を使用した場合の熱抵抗を計算します。

絶縁シートの仕様を見ると、熱伝導率1.2[W/m・K]、厚さ0.3[mm]と記載されています。
これを熱抵抗に変換します。
Rth(sh)=t/(K×L×W)
t ∶ 絶縁シートの厚み [m]
K ∶ 熱伝導率 [W/m・K]
L ∶ ケース接触面の長さ [m]
W ∶ ケース接触面の幅[m]
TO-220パッケージの長さと幅は
L=15[mm]=0.015[m]
W=10[mm]=0.01[m]
Rth(sh)=t/(K×L×W)
=0.0003[m]/(1.2[W/m・K] × 0.015[m] × 0.01[m])
=1.67[K/W](=[℃/W])
これは絶縁シート自体の熱抵抗なので、
絶縁シートの接触部分の熱抵抗は別途存在します。
絶縁シートの有無による熱抵抗の違い
絶縁シートを挟むことで、接触部の熱抵抗が、どの程度大きくなるか実験してみました。
試験条件は先程のグリスの時と同じです。
測定結果は以下になりました。
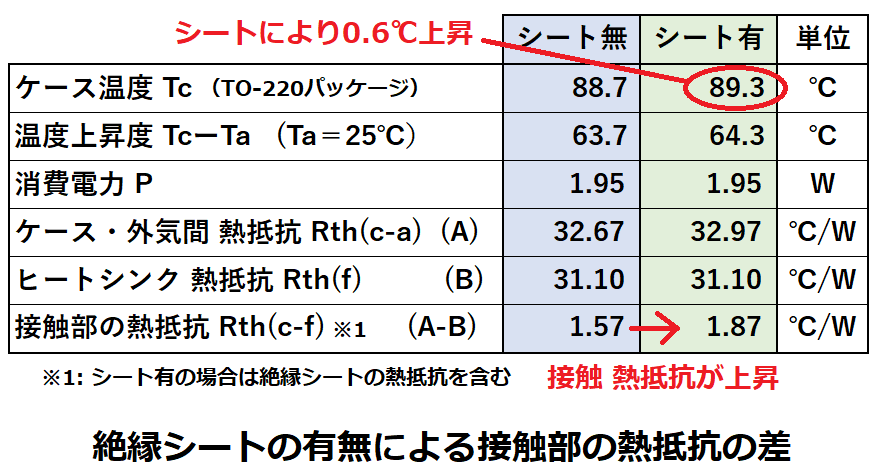
絶縁シートを挟んだ事でケース温度Tcが0.6℃上昇しました。
ケースとヒートシンク間の熱抵抗Rth(c-f)は
絶縁シートがある場合、1.87[℃/W]となりました。
先程、計算した絶縁シートの熱抵抗Rth(sh)が1.67[℃/W]なので、
計算値よりも0.2[℃/W]大きいです。
これは、絶縁シート~ダイオード間 及び、
絶縁シート~ヒートシンク間の接触部分の熱抵抗になります。
このように、接触部の熱抵抗の影響で計算値よりも大きくなりますが、
シート無しの場合と比べ、大きな差が無い事から、
絶縁シートの熱伝導性が優れていることがわかります。
★トランジスタやFETの設計方法についてのまとめ記事です。
★基板の部品交換や修正で役立つ工具類を紹介しています。