この記事でわかること
・サーミスタの種類(NTC、PTC)と選び方
・サーミスタの使い方(温度測定や過電流保護)
・サーミスタを用いた回路設計例
温度によって抵抗値が変化するサーミスタは温度計測だけでなく、
回路の過熱保護や起動時の突入電流制限などにも使用されます。
本記事では、サーミスタの種類と特徴に応じた使い方について具体的な回路例を基に解説します。
本記事はサーミスタを使用する際の基礎知識を説明することが目的であり、
解説する製品の機能や回路の動作を保証するものではありません。
ここで紹介する選定方法が適切で無い場合がある為、
使用の際は、デバイスのデータシートを必ず確認の上、
回路への利用については自己責任でお願いします。
サーミスタの種類
サーミスタ(Thermistor)の名称は「熱に敏感な抵抗 (Thermally Sensitive Resistor)」から来ており、
温度変化により抵抗値が大きく変化する半導体部品で、
熱電対や白金などの他の温度センサより小型で安価なことから広く利用されています。
サーミスタには、温度上昇で抵抗値が減少するNTCと、抵抗値が増加するPTCがあります。
NTCサーミスタ
NTCとは、Negative Temperature Coefficient(負の温度係数)のことで、
温度上昇と共に抵抗値が減少します。
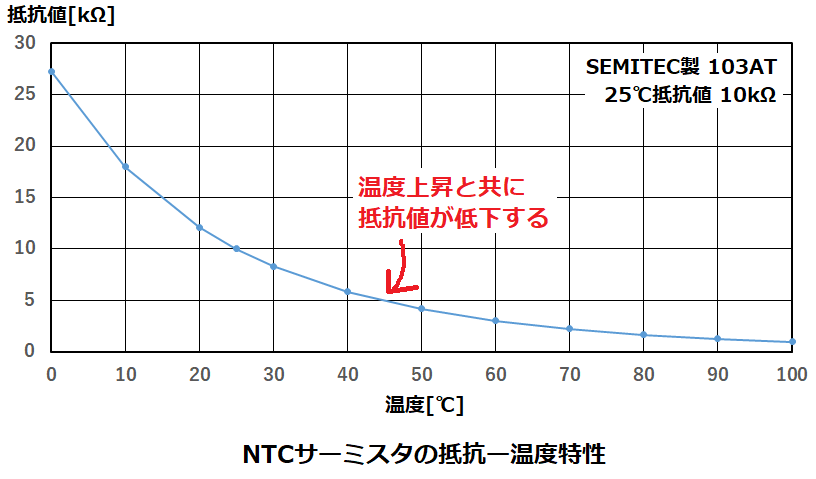
後述するPTCより歴史が古く、単にサーミスタと言えばNTCを指していることが多いです。
また、抵抗ー温度特性がPTCに比べ、広い温度範囲で抵抗値が滑らかに変化するため、
温度センサなどの温度測定に向いています。

また、スイッチング電源等の電源オン時に流れる突入電流の抑制にもNTCが用いられており、
パワーサーミスタとも呼ばれている製品は許容電流が数Aレベルと大きく、
常温(電源オン時)での抵抗値が数Ω~数十Ω程度で突入電流を抑制し、
その後の通電による自己発熱で1Ω以下になることで消費電力を低減できます。

PTCサーミスタ
PTCは、Positive Temperature Coefficient(正の温度係数)なので、
温度が上昇すると抵抗値が増加します。
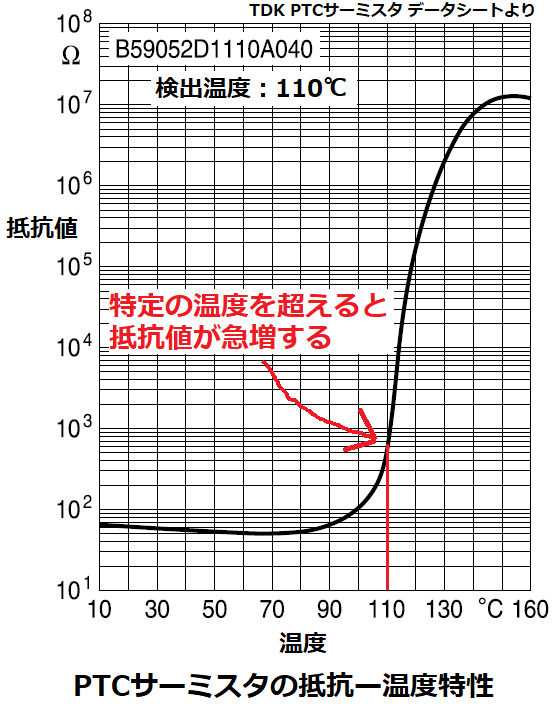
NTCが温度上昇と共に抵抗値が低下するのに対し、PTCは常温付近では殆ど変化せず、
特定の温度を超えると急増する特性となっており、トランジスタやモータ等の過熱検知や、
回路異常で過電流が発生時に電流を制限する回路保護に利用されます。

NTCサーミスタの使い方
サーミスタの抵抗値は次の計算式で求めることができます。

B定数および温度の単位がK(ケルビン)なので、例えば基準温度T0が25℃の場合、
(1)式のT0には25[℃]+273.15=298.15[K]を代入します。
抵抗計算は以下に示すエクセルのEXP関数を使えば簡単に求められます。
EXP関数:自然対数の底e(約2.71828)のべき乗を求める
R=R0*EXP(B(1/(T+273.15)-1/(T0+273.15))) ・・・(2)
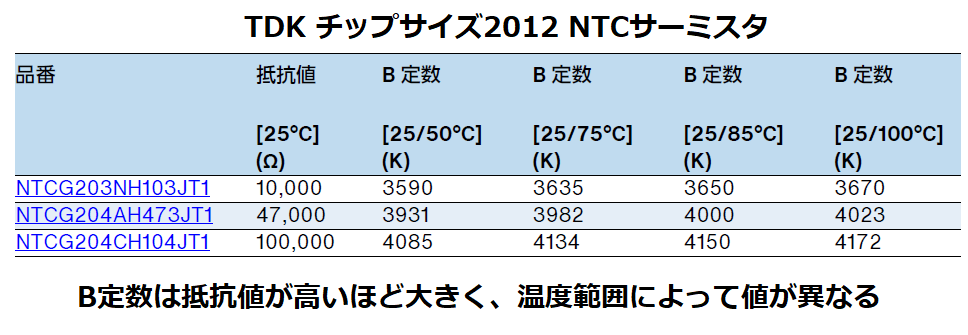
B定数は2点間の温度におけるサーミスタの抵抗変化の割合を表す定数です。

下図にB定数の大きさによる抵抗ー温度特性の違いを示します。
これを見ると、B定数が大きい程、温度変化に対する抵抗変化(感度)が大きくなっています。
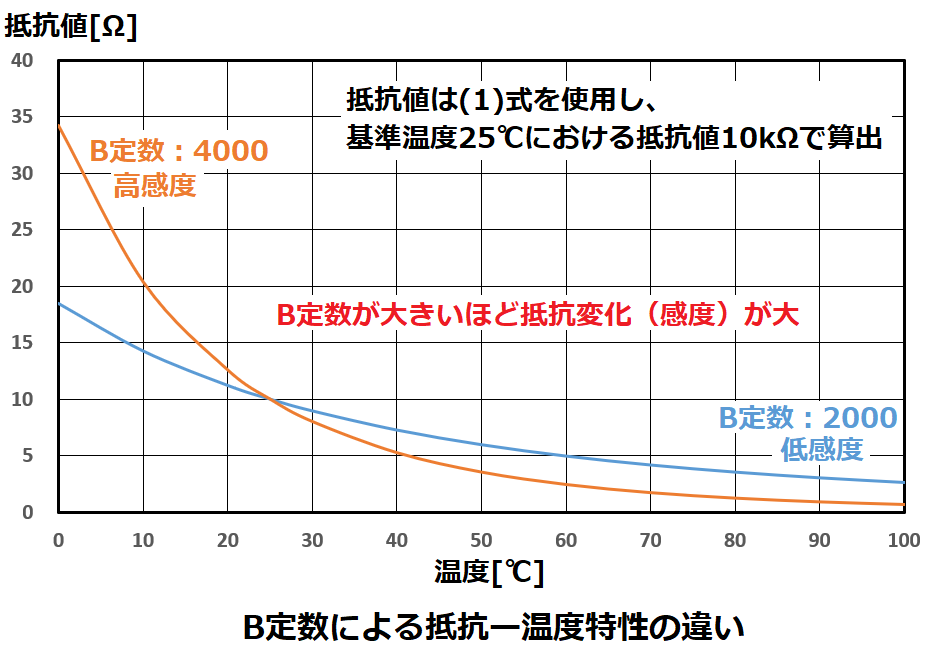
データシートを見ると、抵抗値が高いサーミスタほどB定数が大きい傾向があります。
また、2点間の温度については、T1は85℃、T2が25℃となっているものが多いですが、
(3)式より、B定数は温度範囲(T1,T2)によって値が変化するため、
(1)式の計算を正確に行うには、測定する温度範囲に近いB定数を使用する必要があります。
このように B 定数は一定ではなく、温度上昇と共に少しずつ増加するため、
高精度な温度測定を必要する場合は、各温度における抵抗値が記載されたRT表を用います。
RT表はデータシートに抵抗ー温度特性として掲載されていたり、
メーカーのHPからダウンロードできるものもあります。
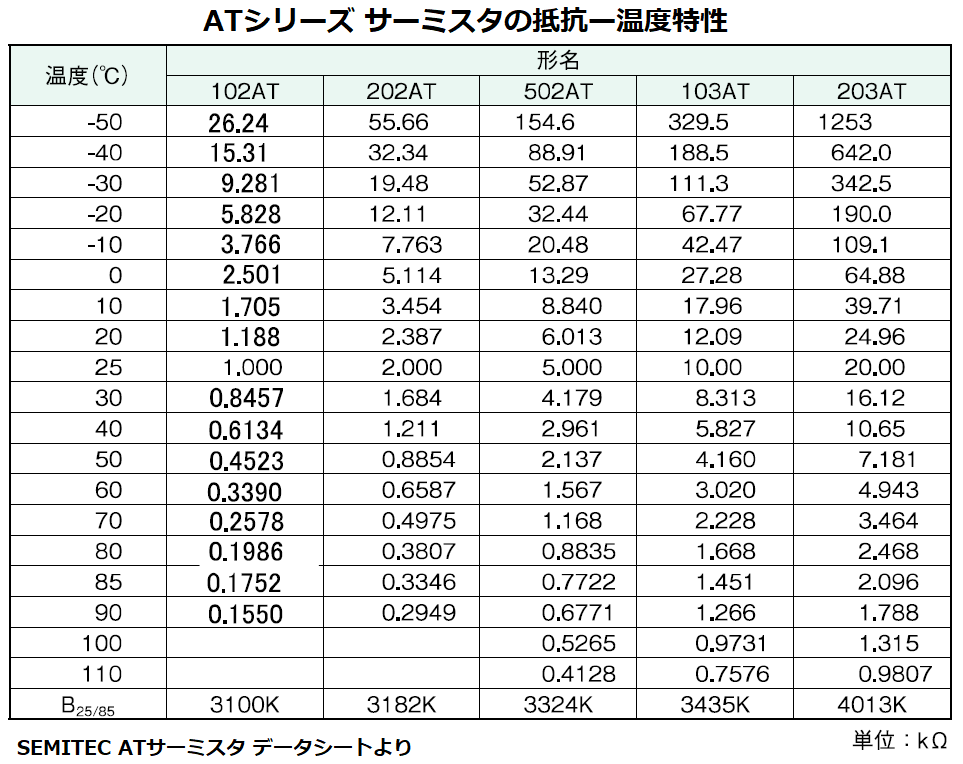
村田製作所のHPでは、各品番の詳細画面に「抵抗温度特性表」として掲載されています。
また、同HP内にある設計支援ソフトウェアSimSurfingのNTCサーミスタ動作シミュレータで
品番を指定し、シミュレートした画面上にある「R-T Curve of Thermistor(reference)」グラフ
のCSV出力ボタンを押すと抵抗ー温度特性のCSVファイルがダウンロードできます。
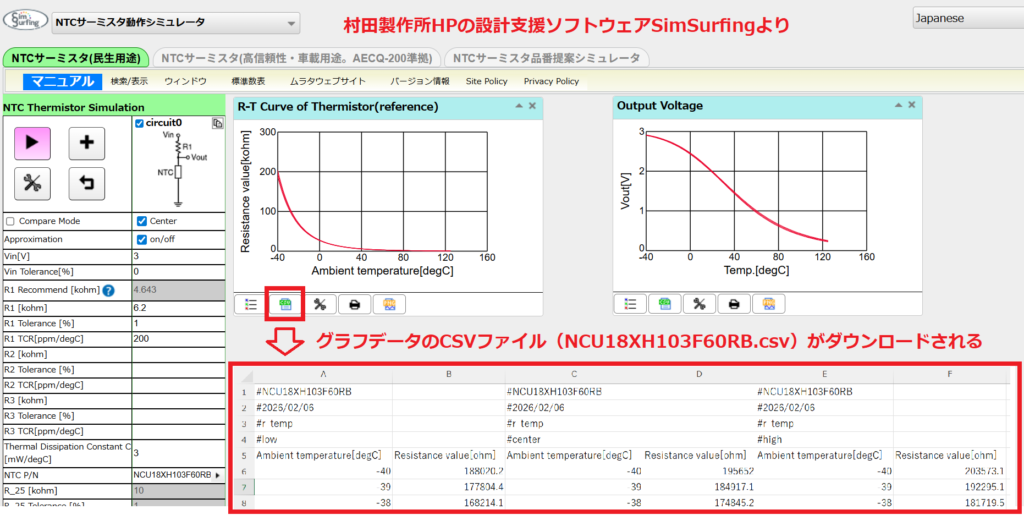
B定数の他に、データシートに記載されている定数に以下のものがあります。
熱放散定数
サーミスタ自身が通電による自己発熱によって1℃温度上昇するのに必要な消費電力を表します。
例えば、SEMITEC製103AT(抵抗値10kΩ)の熱放散定数は2mW/℃なので、P=I2×Rを変形して
I=√(2mW/10kΩ)≒0.45mAの電流がサーミスタに流れると、温度が1℃上昇します。
これによって、実際の周囲温度より1℃高い温度の抵抗値となり、測定誤差となってしまいます。
従って、熱放散定数が大きいサーミスタほど、自己発熱による影響を小さくできます。
サーミスタに流れる電流が小さくすれば、自己発熱による測定誤差を減らせるので、
この後で解説する温度計測回路の入力電圧を低くすれば良いのですが、
その分計測される出力電圧は小さくなる欠点があります。
熱時定数
温度変化に対するサーミスタの応答性を表す定数で、周囲温度がT1からT2まで上昇した時に、
サーミスタの温度が温度差(T2ーT1)の63.2%まで上昇する時間を示します。
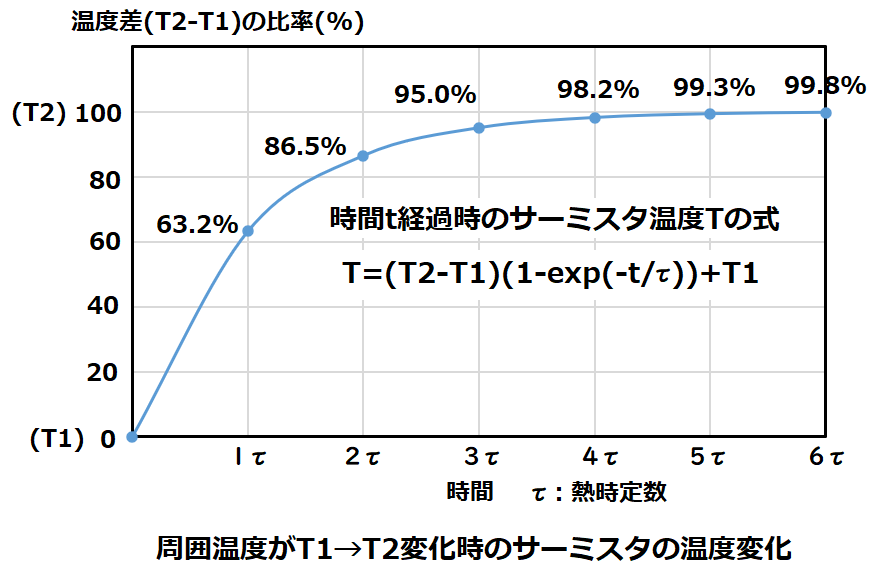
このため、サーミスタで周囲温度を測定するには、この熱時定数より長い時間にする必要があり、
一般的には応答時間を熱時定数の3倍(95.0%)か、5倍(99.3%)にします。
例として、103AT-2の熱時定数は15sなので、応答時間を5倍とすると75s(1分15s)と長いです。
更に、同じ103ATでもリード線がついたサイズの大きい103AT-11だと熱時定数が75sなので、
5倍で375s(6分15s)と非常に長い時間になってしまいます。
このように熱時定数は部品サイズが小さいほど短くなる傾向である(※)ため、
応答性を良くするなら小型のサーミスタを使用します。
※非常に小型であるチップタイプには熱時定数が記載されていないものが多い。
但し、部品サイズが小さいと熱放散定数が小さくなる傾向があるので、
温度検出精度と応答性のバランスを考慮して選定します。
NTCサーミスタを使った温度計測回路
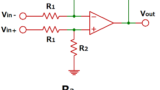
サーミスタの抵抗ー温度特性は直線性がありませんが、
固定抵抗で分圧した電圧を測定することで、
電圧ー温度特性にある程度の直線性を持たせることができます。
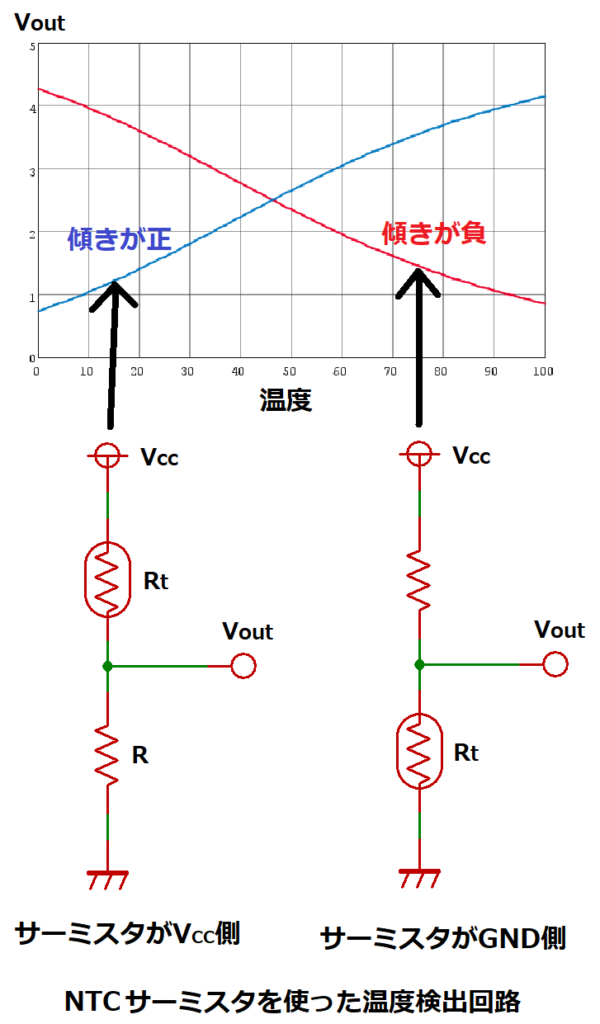
固定抵抗との分圧回路は、サーミスタの配置によって特性が異なります。
サーミスタがVcc側:温度上昇により出力電圧が上昇(グラフの傾きが正)
サーミスタがGND側:温度上昇により出力電圧が下降(グラフの傾きが負)
ここでは、直観的に扱いやすいサーミスタがVcc側の場合について説明すると、
出力電圧Voutは下記式となります。
Vout=Vcc×R/(Rt+R)・・・(4)
Vcc:入力電圧
Rt:サーミスタの抵抗値
R:固定抵抗値
Rを求める方法については、次の3つを紹介します。
<方法1>
測定温度範囲におけるVoutー温度特性の直線性が高くなるRを求める方法です。
R=[RtM(RtL+RtH)ー2RtL・RtH]/[(RtL+RtH)ー2RtM] ・・・(5)
RtL:測定温度範囲の最低温度でのサーミスタ抵抗値
RtH:測定温度範囲の最高温度でのサーミスタ抵抗値
RtM:測定温度範囲の中間温度でのサーミスタ抵抗値
<方法2>
測定温度範囲内でVoutの変化が最大になるRを求める方法です。
R=√(RtL×RtH)・・・(6)
<方法3>
基準温度(25℃)でのVoutが出力可能な電圧範囲の中央になるRを求める方法です。
R=サーミスタの25℃における抵抗値
<(5)式となる理由>
RtL、RM、RtHにおける各出力電圧(VoutH、VoutH、VoutH)を(4)式より求めます。
VoutH=Vcc×R/(RtH+R)
VoutM=Vcc×R/(RtM+R)
VoutL=Vcc×R/(RtL+R)
Voutが温度変化に対し直線性(比例)がある場合、
VoutM ー VoutL =VoutH ー VoutM が成立します。
この式を変形すると、
2VoutM = VoutH + VoutL
となるので、これに各温度における出力電圧の式を代入します。
2Vcc×R/(RtM+R)=Vcc×R/(RtH+R)+Vcc×R/(RtL+R)
この式をRの式になるように変形すると
R=[RtM(RtL+RtH)ー2RtL・RtH]/[(RtL+RtH)ー2RtM]
となり、(5)式となります。
<(6)式となる理由>
サーミスタの抵抗値が測定温度範囲(最低温度~最高温度)で変化した時、
出力電圧Voutの変化が入力電圧範囲(Vcc~GND)内で最も大きくなるように、
最低温度と最高温度におけるVoutの差ΔV=VoutHーVoutLが最も大きくなるRを求めます。
これはΔVをRを変数とした関数の極大値を求めることになり、
ΔVーRをグラフで表した場合、山(ピーク)の部分に相当し、
グラフの傾きがゼロになる時(※)です。
※極小値(グラフの谷)の部分でも傾きがゼロになります。
この時、傾きゼロとなる位置の前後で、傾きが正から負に変わる場合は極大値、
負から正に変わる場合は極小値になります。
まず、各温度における出力電圧の式を代入します。
ΔV=VoutHーVoutL=Vcc×R/(RtH+R)ーVcc×R/(RtL+R)
=Vcc×R(1/(RtH+R)ー1/(RtL+R))
関数ΔVの傾きを求めるため、ΔVの式をRについて微分すると(※)
d/dR (ΔV)=[RtH・RtL2ーRtL・R2ーRtH2・RtL+RtH・R2]/[RtH・RtL+RtH・R+RtL・R+R2]2
この微分した値がゼロになるには分子がゼロの時なので、
RtH・RtL2ーRtL・R2ーRtH2・RtL+RtH・R2=0
R2(RtHーRtL)=RtH・RtL(RtHーRtH)
R=√(RtH・RtL)
となり、(6)式となります。
※微分は「d/dx (x⋅( 1/(A+x) – 1/(B+x) ))」をgoogleで検索すると解法が提示されるので参考にして下さい。
この回路に、SEMITECのATシリーズ サーミスタ103ATを使用して、
測定温度範囲が狭い(0~50℃)場合と、広い(0~100℃)の場合の計算例を示します。
<計算例1(0~50℃)>
サーミスタ103ATのデータシートより、各温度の抵抗値は以下になります。
RtL=27.28kΩ(0℃)
RtM=10kΩ(25℃)
RtH=4.160kΩ(50℃)
固定抵抗Rの値については、方法1((5)式)を使用した場合、
R=[RtM(RtL+RtH)ー2RtL・RtH]/[(RtL+RtH)ー2RtM]
=[10(27.28+4.16)ー2×27.28×4.16]/[(27.28+4.16)ー2×10]
=(314.4ー226.9696)/(31.44ー20)
=87.4304/11.44 ≒ 7.643kΩ
方法2((6)式)を使用した場合は、
R=√(RtL×RtH)=√(27.28×4.16) ≒ 10.653kΩ
(4)式に当てはめると
方法1((5)式)の場合 Vout=Vcc×7.643kΩ/(Rt+7.643kΩ)
方法2((6)式)場合 Vout=Vcc×10.653kΩ/(Rt+10.653kΩ)
方法3はサーミスタ103ATの25℃における抵抗値10kΩをRとします。
方法3の場合 Vout=Vcc×10kΩ/(Rt+10kΩ)
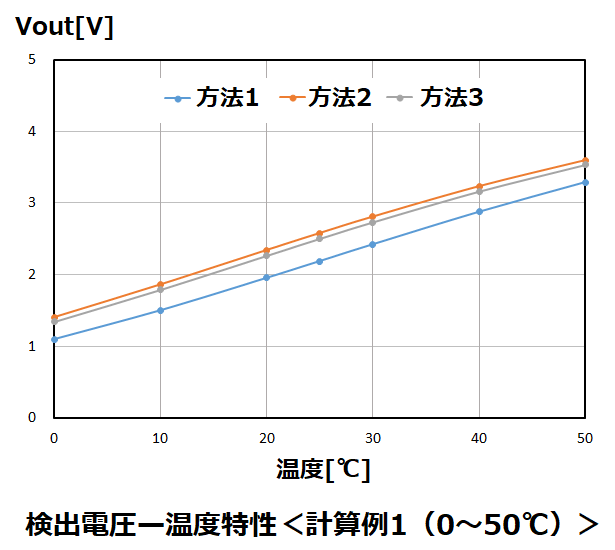
各方法において、Vcc=5VでVoutを算出した結果を示します。
<計算例2(0~100℃)>
計算例1と同様の手順で求めます。
RtL=27.28kΩ(0℃)
RtM=4.160kΩ(50℃)
RtH=0.9731kΩ(100℃)
抵抗Rは方法1((5)式)の場合、3.233kΩ、
方法2((6)式)の場合は5.152kΩ、方法3は計算例1と同じ10kΩです。
計算例1と同様に算出した結果は以下となります。
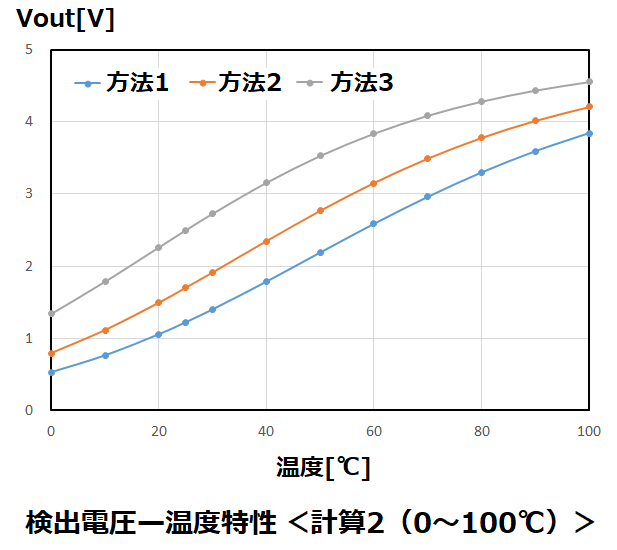
両グラフを比較すると、温度範囲が狭い場合は、各方法に大差はありませんが、
温度範囲が広くなると、方法1の直線性が際立つようになります。
この結果より、温度範囲が25℃付近の狭い測定では、簡単な方法3でも良いですが、
広い温度範囲で測定誤差を小さくした場合は方法1が適しています。
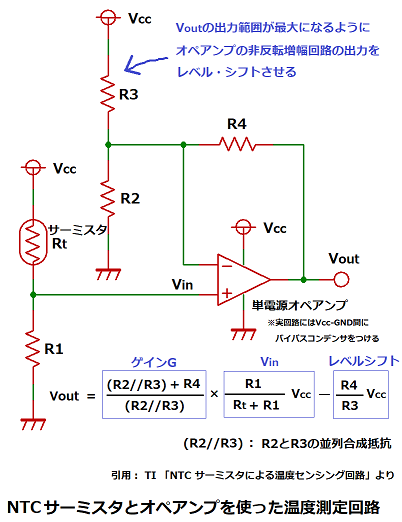
オペアンプを使った増幅回路
前述した固定抵抗との分圧回路では、測定温度範囲でのVoutの変化幅が小さいため、
オペアンプを使用して、信号の増幅とレベルシフトを行うことで、
Voutを電源電圧VccからGNDまで幅いっぱいに変化するようにします。
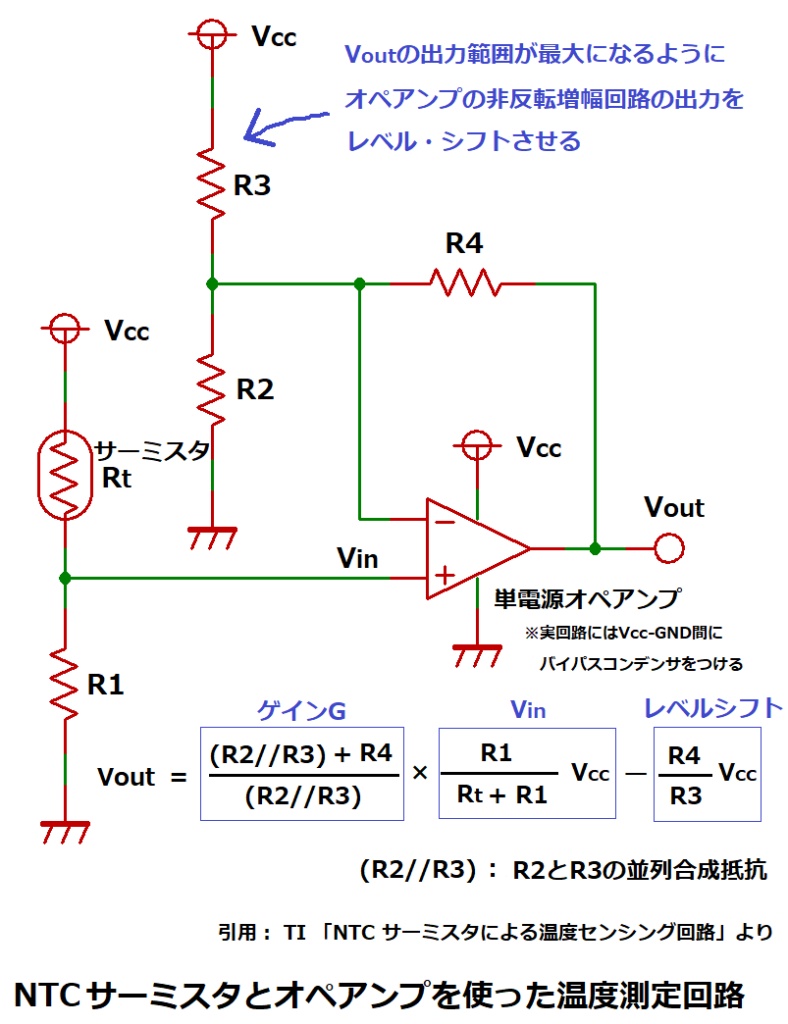
これにより、1℃あたりのVoutの電圧変化が大きくなるので、
温度変動の検出精度を高めることができます。
この回路は、NTCサーミスタによる温度検出電圧を、レール・ツー・レール入出力の
単電源オペアンプ(※)を使用した非反転増幅回路で増幅し、
VoutがVcc~GND間で出来るだけ幅広く変化するように出力をシフトしています。
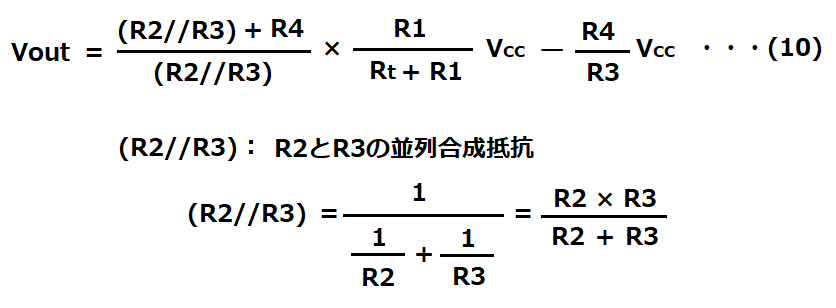
※(10)式になる理由については後述します。
※レール・ツー・レールのオペアンプについては下記記事で解説しています。
選定したオペアンプの出力電圧範囲が0.1V~Vccー0.1Vとすると、
Vccを5Vに設定した場合、Voutは0.1V~4.9Vまで出力可能なので、
設定した2つの温度範囲内で、Voutが上記範囲内いっぱいに使えるように
各抵抗値を設定します。
①Vinの範囲が最大になるようにR1を求める
測定温度範囲を0℃~50℃とした場合、
前述した計算例1の方法2を使って求めた10.653kΩを基にして、
E96系列(※)から10.7kΩを選定します。
※E96系列の抵抗値は精度1%以上の高精度品になりますが、
安価で入手しやすいE24系列の抵抗値で選定すると、理想値との差が大きくなり、
この後のVout算出で、オペアンプの出力電圧範囲から外れてしまう場合があります。
②Vinの範囲を求める
Vin=Vcc×R1/(Rt+R1)より、Vinの上下限値を算出します。
(0℃と50℃のサーミスタ抵抗Rtは計算例1の値を使用)
Vin(min)=5V×10.7kΩ/(27.28kΩ+10.7kΩ)
≒1.409V(0℃の場合)
Vin(max)=5V×10.7kΩ/(4.160kΩ+10.7kΩ)
≒3.600V(50℃の場合)
③Voutの範囲が最大になるようにゲインGを求める
VinがVin(min)からVin(max)まで変化した時に、
Voutがオペアンプの出力電圧範囲(0.1V~4.9V)まで変化させるのに必要なゲインGは
G=(Vout(max)ーVout(min))/(Vin(max)ーVin(min))
=(4.9ー0.1)/(3.600ー1.409)
=4.8/2.191 ≒ 2.191
④各抵抗値を求める
この回路のゲインは(10)式より、G=((R2//R3)+R4)/(R2//R3)なので、
R4=1.5kΩにした場合(※)、並列合成抵抗(R2//R3)は、
(R2//R3)=R4/(Gー1)
=1.5kΩ/(2.191ー1)
≒1.259kΩ
※抵抗値が大きくなるとノイズが発生しやすくなるので10kΩ 以下が望ましい。
次にR2とR3を求めます。(10)式は以下の様に表現できます。
Vout=G×VinーR4/R3
最大温度(50℃)の場合は(※) ※最低温度(0℃)の場合で計算しても結果は同じ。
Vout(max)=G×Vin(max)ーR4/R3
なので、R3の式に変形すると
R3=R4×Vcc/(Vin(max)×GーVout(max))
=1.5kΩ×5V/(3.600V×2.191ー4.9V)
≒ 2.510kΩ
次にR2は、(R2//R3)=(R2×R3)/(R2+R3)より
R2=(R2//R3)×R3/(R3ー(R2//R3))
=1.259kΩ×2.510kΩ/(2.510kΩー1.259kΩ)
≒2.526kΩ
E96系列より、R2=2.55kΩ、R3=2.55kΩを選択すると、
(R2//R3)=(R2×R3)/(R2+R3)
=(2.55k×2.55k)/(2.55k+2.55k)
=1.275kΩ
G=1+R4/(R2//R3)
=1+1.5kΩ/1.275kΩ
≒2.176
従って、出力電圧Voutは以下の式となります。
Vout=G×VinーR4×Vcc/R3
=2.176×Vinー1.5kΩ×5V/2.55kΩ
≒2.176×Vinー2.941V
Voutの上下限値を計算すると
Vout(min)=2.176×Vin(min)ー2.941V
=2.176×1.409Vー2.941V
≒0.12V(0℃の場合)
Vout(max)=2.176×Vin(max)ー2.941V
=2.176×3.600Vー2.941V
≒4.89V(50℃の場合)
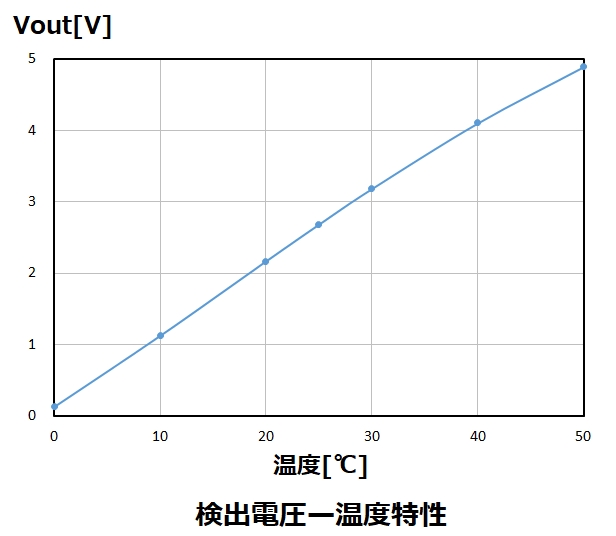
以上から、0℃~50℃に温度変化した場合、
出力電圧Voutは0.12V~4.89Vまでほぼ直線的に変化します。(下図参照)
<(10)式になる理由>
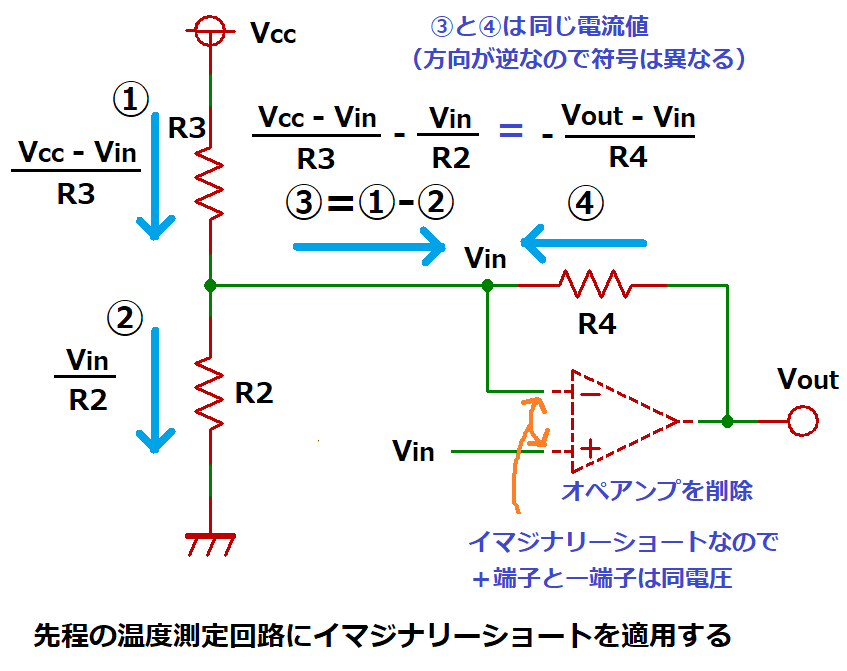
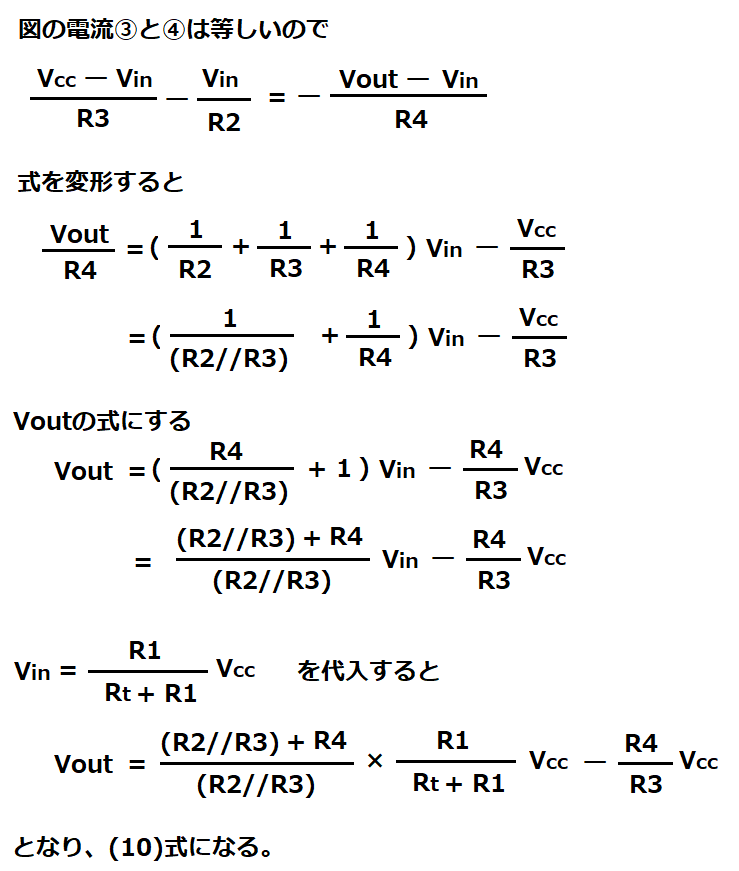
負帰還(出力がー入力に戻る)の構成をしたオペアンプは
反転入力端子(-)と非反転入力端子(+)が同じ電圧(※)になるように
出力端子から電圧が出力されます。
この考え方を回路に適用すると、ー端子と+端子は同じ電圧となり、
オペアンプの三角記号を削除して、電圧や電流を計算できます。
※この考え方をイマジナリーショート(仮想短絡)と呼びます。
オペアンプを使った負帰還増幅回路は、このイマジナリーショートを適用して、
出力電圧を求めることができます。
オペアンプの使い方については下記記事で解説しています。
パワーサーミスタを使った突入電流防止回路
AC/DC電源にはAC電圧をDC電圧に変換する全波整流回路があり、
ブリッジ・ダイオードと平滑コンデンサから構成されています。
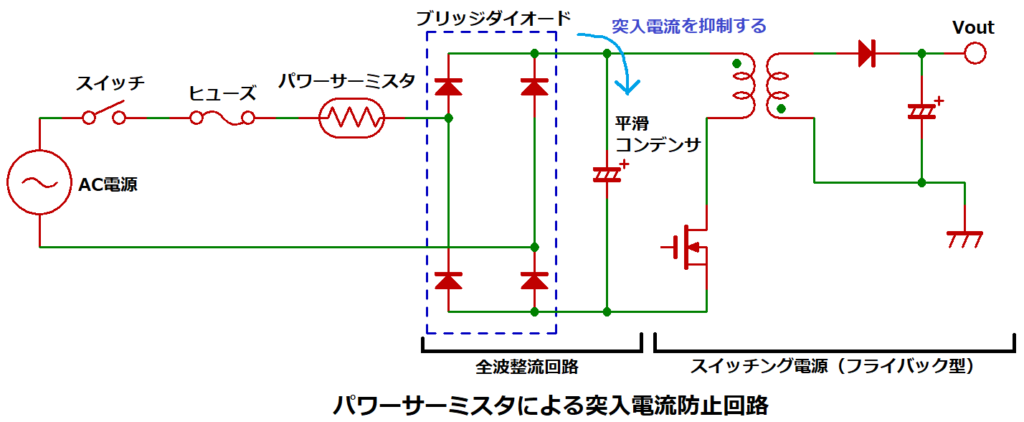
平滑コンデンサはブリッジダイオードで全波整流した電圧を一定にするため
大容量の電解コンデンサが用いられていることから、
電源投入時、未充電のコンデンサには大きな充電電流(突入電流)が流れます。
この突入電流はブリッジダイオード等の周辺部品に損傷を与える場合があるため、
パワーサーミスタを接続して、電源投入時は数Ω~十数Ω程度の抵抗で電流を制限し、
通電による温度上昇で小数点以下の微小抵抗となることで、損失を低減します。
但し、電源オフ後に温度が下がらないうちにオンすると抵抗が小さいままなので、
突入電流が流れてしまうことから、オン/オフを頻繁に繰り返す用途には向きません。(※)
※この問題を回避する方法として、電源オン時は抵抗を経由し、
その後は抵抗間を短絡するためのリレーやサイリスタなどを設けますが、
それらをオン・オフするための制御回路が必要となります。
パワーサーミスタはブリッジダイオードの前に接続するのが一般的ですが、
突入電流が流れる箇所に設ければ良いので、平滑コンデンサの前であれば、
ブリッジダイオードの後に接続しても良いです。

パワーサーミスタは次の3つの条件を満たすものを選び、
実際に電流や温度を測定して、定格に対し余裕があるか確認して決めます。
①使用する回路の最高周囲温度におけるサーミスタ抵抗値で流れる電流が
周辺部品(※)の許容電流以下になること
※上の回路図では、スイッチ、ヒューズ、ブリッジダイオードになります。
ブリッジダイオードについては、非繰り返し順方向電流の最大許容値である
せん頭サージ順電流より十分小さくなるようにします。
入力AC電圧(実効値)をVAC(rms) 、周辺部品の許容電流をIPとすると、
最高周囲温度Ta(max)において必要となるサーミスタ抵抗値RTa(max)は、
RTa(max)=VAC(rms) × √2 /IP
データシートに記載されているサーミスタ抵抗値は25℃時なので、
RTa(max)を25℃時の抵抗値R25に換算します。
B定数がわかれば、(1)式を変形することでR25が求まりますが、
ここでは計算を簡単にするため次の手順で求めます。
まず、(2)式を使って、R0(T0=25℃時の抵抗値)を1Ωにして、
温度Ta(max)時の抵抗値RTa(max)(R0=1Ω)を計算します。
ここで求めたRTa(max)(R0=1Ω)は、抵抗値が25℃の時に比べ、
Ta(max)時は何%に減少するかを意味するので、次式で表現できます。
RTa(max)=R25×RTa(max)(R0=1Ω)
この式を変形すると、
R25[Ω]=RTa(max)/RTa(max)(R0=1Ω)
となり、Ta(max)時の抵抗値がRTa(max)となるサーミスタが、
25℃になった時の抵抗値R25を算出できます。
②最高周囲温度におけるサーミスタの許容電流が
回路の負荷電流(サーミスタに流れる定常電流)より大きいこと
許容電流は、サーミスタに連続して流せる最大電流のことで、
一般的には周囲温度条件が25℃で規定されており、
周囲温度が高いほど、許容電流は低下します。
ここでは下記式を用いて、最高周囲温度Ta(max)における許容電流Imax(Ta)を求めますが、
メーカーから提示された電流値や算出方法がある場合は、それに従います。
Imax(Ta)[A]=Imax(25)×(1ー(Taー25)/(Tmaxー25))
Imax(25):周囲温度25℃時の許容電流[A]
Ta:最高周囲温度[℃](但し、25℃以上)
Tmax:サーミスタの使用温度範囲の上限値[℃]
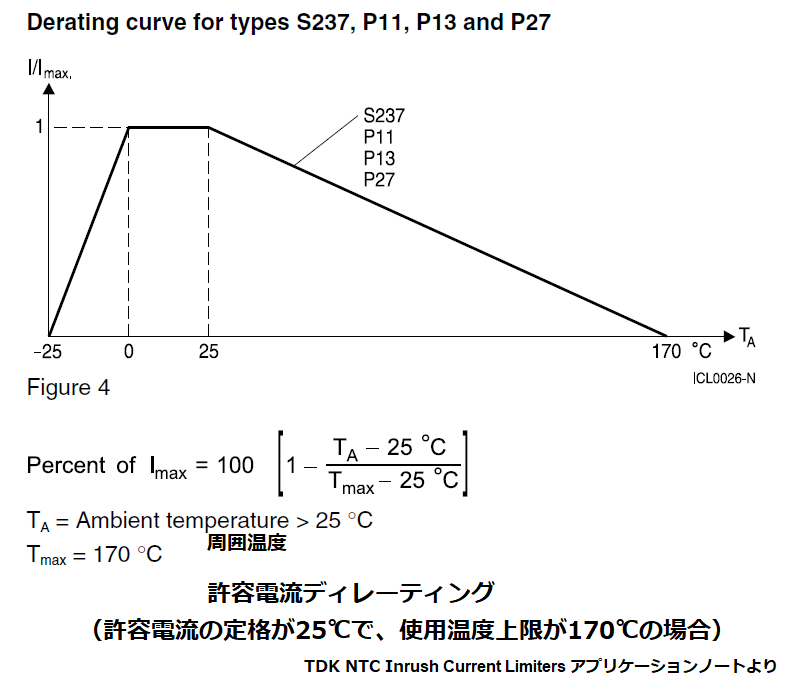
③使用する回路の入力電圧におけるサーミスタの許容コンデンサ容量が
回路の平滑コンデンサ容量より大きいこと
データシートに記載されている許容コンデンサ容量には
入力電圧条件としてAC100VやAC240Vなどが規定されていることから、
使用する回路の入力電圧に換算時の許容コンデンサ容量Cinは下記式で求めます。
Cin [μF]=Ctest ×(Vtest(rms) × √2)2 / (Vin(rms) × √2)2
Ctest :データシート記載の許容コンデンサ容量[μF]
Vtest(rms) :Ctest の入力電圧条件(実効値)[V]
Vin(rms) :使用する回路の入力電圧(実効値)[V]
この式になる理由ですが、サーミスタに接続するコンデンサが
蓄えることができるエネルギーは入力電圧が違っても同じとすると、
コンデンサに蓄えるエネルギーの公式Q=CV2/2より、
Cin ×(Vin(rms) × √2)2/2=Ctest ×(Vtest(rms) × √2)2 /2
となり、この式を変形すると、先程のCin の式になります。
例として、下記仕様の回路において3つの条件を求めます。
最高周囲温度Ta(max):60℃
入力電圧Vin(rms) :AC100V
回路の許容電流IP:30A
条件①
最高周囲温度Ta(max)において必要となるサーミスタ抵抗値RTa(max)は、
RTa(max)=VAC(rms) × √2 /IP
=100V× √2 /30A≒4.72Ω
使用するサーミスタのB定数が3000の場合、
(2)式を使って、25℃時の抵抗値を1Ωとした時の
温度60℃時の抵抗RTa(max)(R0=1Ω)を計算すると、
RTa(max)(R0=1Ω)≒0.347Ω
25℃時のサーミスタ抵抗値R25は、
R25=RTa(max)/RTa(max)(R0=1Ω)
=4.72Ω/0.347Ω≒13.6Ω
従って、R25が13.6Ω以上のサーミスタを選定します。
条件②
サーミスタの周囲温度25℃時の許容電流が3A、使用温度の上限が170℃の場合、
周囲温度60℃における許容電流Imax(Ta)は、
Imax(Ta)[A]=Imax(25)×(1ー(Taー25)/(Tmaxー25))
=3A×(1ー(60ー25)/(170ー25))
=3A×(1ー35/145) ≒ 2.2A
従って、このサーミスタを使用した場合、
回路の負荷電流は2.2A以下でなくてはなりません。
条件③
使用するサーミスタのAC240Vにおける許容コンデンサ容量が120uFの場合、
入力電圧AC100Vにおける許容コンデンサ容量Cinは、
Cin [μF]=Ctest ×(Vtest(rms) × √2)2 / (Vin(rms) × √2)2
=120×(240× √2)2 / (100× √2)2 ≒ 690uF
従って、このサーミスタを使用した場合、
平滑コンデンサ容量は690uF以下にする必要があります。
※平滑コンデンサの容量の決め方については下記記事で解説しています。
PTCサーミスタの使い方
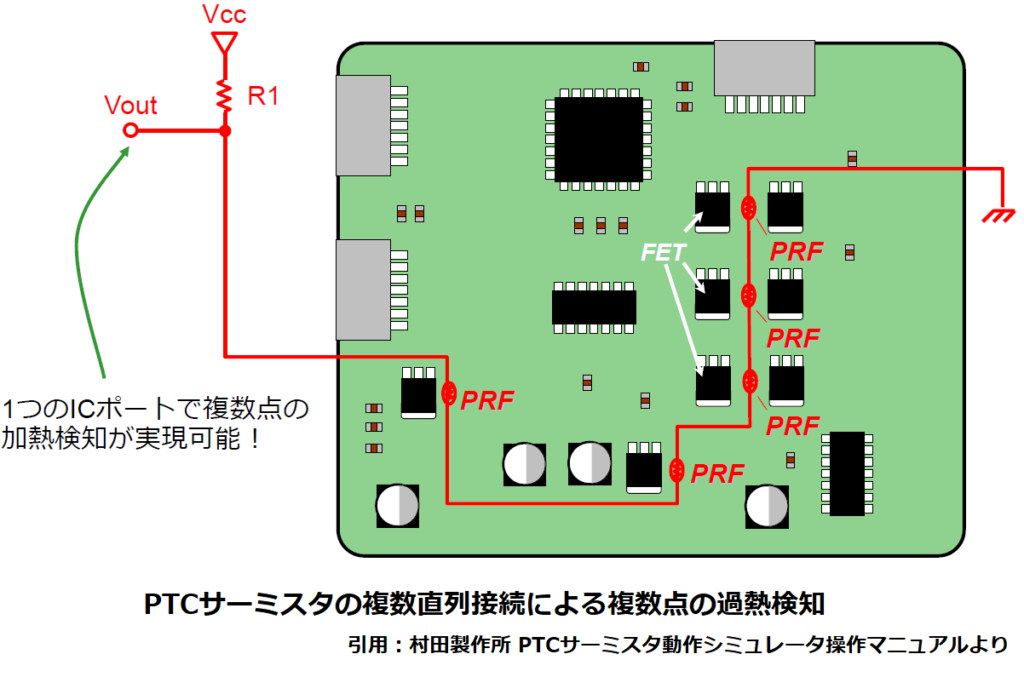
PTCサーミスタを過熱検知に使用する場合、通常は図に示すように
上側を抵抗、下側をサーミスタにした直列回路で分圧した電圧Voutが、
PTCの抵抗温度特性により、温度上昇に伴い指数関数的に上昇することで検出します。
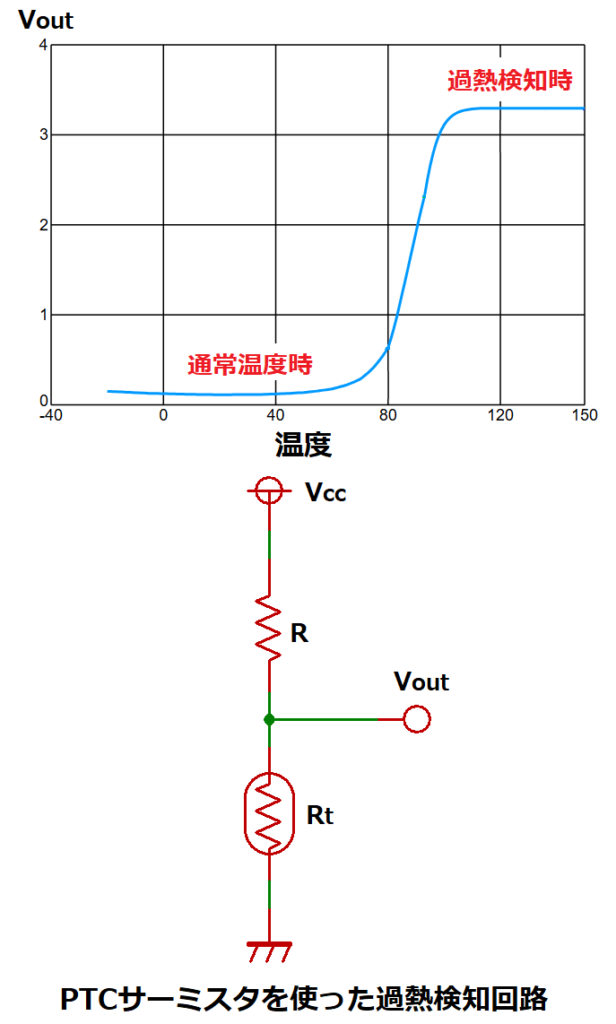
ここでは、村田製作所の過熱検知用PTCサーミスタPRF18シリーズを用いて
サーミスタが100℃付近になったら過熱検知を行う回路について説明します。
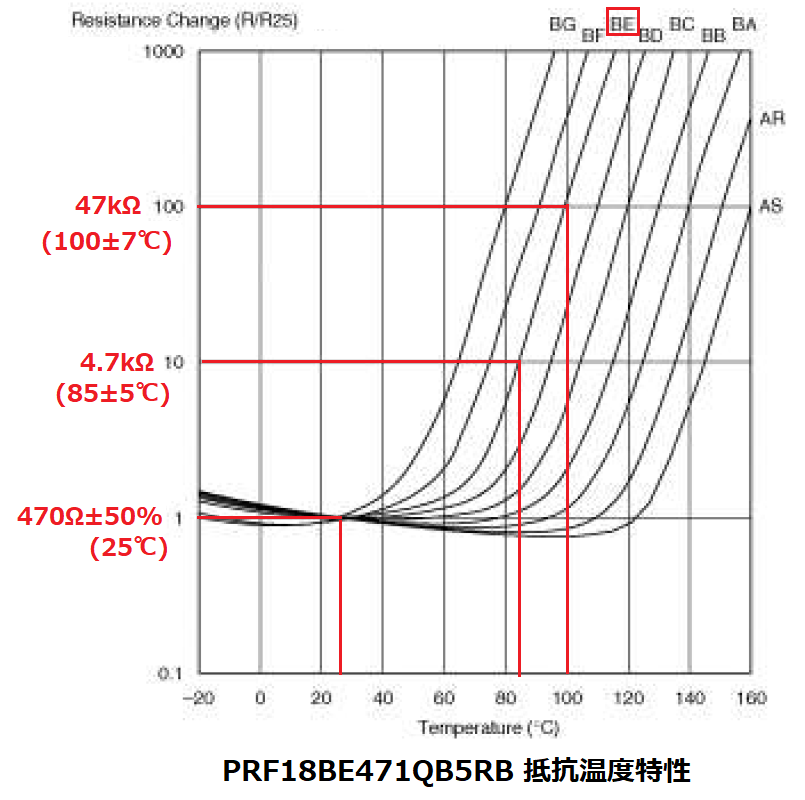
このサーミスタは25℃の抵抗値が470Ωで、抵抗値が10倍の4.7kΩになる検知温度と、
100倍の47kΩになる検知温度の2つが規定されています。
(本記事では、抵抗10倍を検知温度1、100倍を検知温度2と称することにします)
この2つの検知温度は精度が異なり、
抵抗10倍の検知温度1が±5℃、100倍の検知温度2が±7℃です。
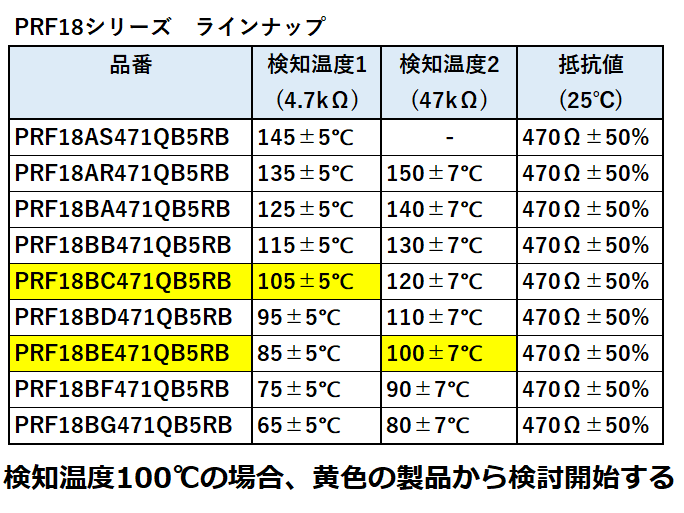
PRF18シリーズのラインナップを見ると、検知温度が100℃付近なのは、
検知温度1(4.7kΩ)が105±5℃のPRF18BC471QB5RBと、
検知温度2(47kΩ)が100±7℃のPRF18BE471QB5RBの2つから選べます。
温度精度を求めるなら検知温度1を使い、
抵抗(電圧)変化の大きさを求めるなら検知温度2を使いますが、
ここでは検知温度2のPRF18BE471QB5RBにします。
Voutをマイコン等のデジタル入力で検出する場合、通常のCMOSレベルでは、
Hレベル入力電圧VIH=0.7×Vcc、Lレベル入力電圧VIL=0.3×Vcc なので、
Vccが3.3Vだと、VIH=2.31V、VIL=0.99Vとなるため、
Voutが通常時は0.99V以下で、過熱検出時は2.31V以上になるように抵抗を選びます。
検知温度2(47kΩ)の時のVoutがHレベル(2.31V)になので、
Vout=Rt/(Rt+R)×Vcc
=47kΩ/(47kΩ+R)×3.3V=2.31V
式を変形すると、R≒20kΩになります。
各温度のVoutを算出すると、
100℃時 Vout=47k/(47k+20k)×3.3 ≒ 2.31V
85℃時 Vout=4.7k/(4.7k+20k)×3.3 ≒ 0.63V
25℃時 Vout=470/(470+20k)×3.3 ≒ 0.07V
となり、100±7℃の時にHレベル電圧、85±7℃は0.63VなのでLレベル電圧となり、
100℃付近で過熱検知をすることができます。
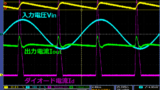
下図は村田製作所HP内にある設計支援ソフトウェアSimSurfingの
PTCサーミスタ動作シミュレータで確認した波形です。
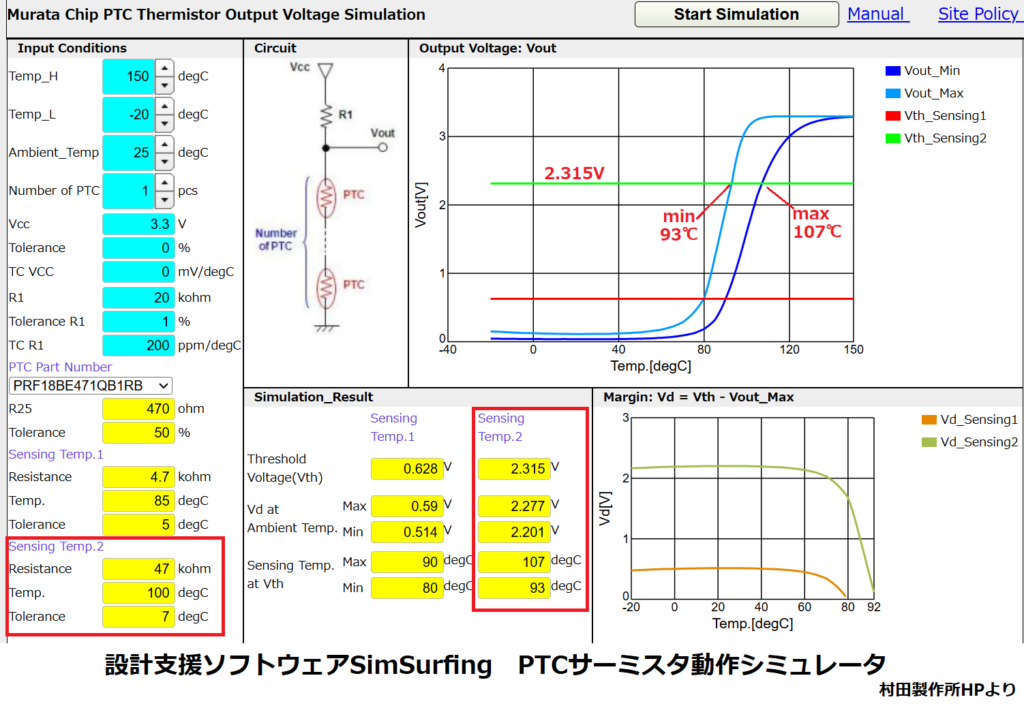
シミュレータの回路図にあるように複数のPTCサーミスタを直列に接続することで、
ひとつのVoutで複数箇所の過熱検出を行うことができます。