この記事でわかること
・電流センサの種類と原理
・カレントトランス(CT)の使い方と選び方
・CTによる電流検出回路
カレントトランス(CT)を用いた電流センサは、
電源を必要とせず、電線をCTの貫通孔に通すことで、
測定対象となる回路とは絶縁した状態で交流電流を検出できます。
本記事では、CTの原理や用途を、他の電流検出法との違いや特徴から解説し、
CTの選定方法や、具体的な電流検出回路についても紹介します。
本記事はCTによる電流センサ設計の基礎知識を説明することが目的であり、
解説する製品の機能や回路の動作を保証するものではありません。
ここで紹介する方法が適切で無い場合がある為、
使用の際は、デバイスのデータシートを必ず確認の上、
記事にある回路の利用については自己責任でお願いします。
電流センサの種類と原理
電流検出方法には大別して、以下の3つがあります。
・シャント抵抗を用いる方法
抵抗に電流が流れることによる電圧降下を利用して、
V=R×Iより、検出電圧Vを基に電流Iを求めます。
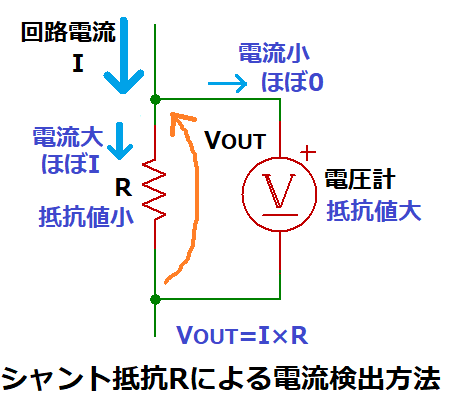
この時、抵抗Rに対し並列に電圧計を接続するため、回路電流Iは分流されますが、
電圧計の内部抵抗は非常に大きく、Rを低抵抗にすることで、
Rに流れる電流=回路電流Iとなります。
この「分流する」という意味のシャント(Shunt) より、
電流検出用の低抵抗をシャント抵抗と呼びます。
この方法は高精度抵抗を用いることで、検出精度を高めることができ、
AC(交流)だけでなく、DC(直流)も検出できます。
シャント抵抗による回路への影響(電圧降下や消費電力)を小さくするため、
抵抗値は数Ω以下にするのが一般的ですが、
それでも、大電流を流すと抵抗の発熱(損失)が大きくなるので、
定格電力が数W以上の抵抗が利用されます。

シャント抵抗に用いられる抵抗の種類としては、
リード部品の場合はセメント抵抗などの電力型が用いられ、
チップ部品では、厚膜型や金属板型があります。
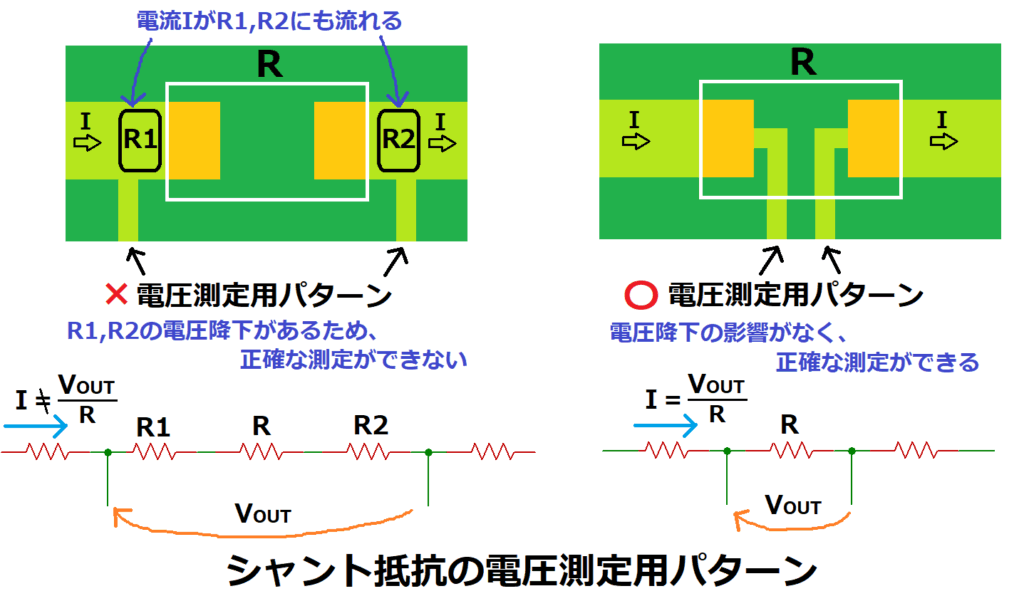
また、抵抗値が低い程、配線の抵抗成分による影響が大きいため、
電圧測定用のパターンについては図に示す様な引き回しにします。
・カレントトランス(CT)を用いる方法
トランスの一次側に流れる電流によって二次側に発生する電圧を計測する方法で、
測定対象となる回路とは絶縁した状態で電流を検出できます。

この方法は電源を必要とせず、電線をトランスのコアに通すだけで
検出電圧が出力されますが、交流しか検出できないため、
直流電流を回路と絶縁して検出する場合は、後述するホール素子を使用します。
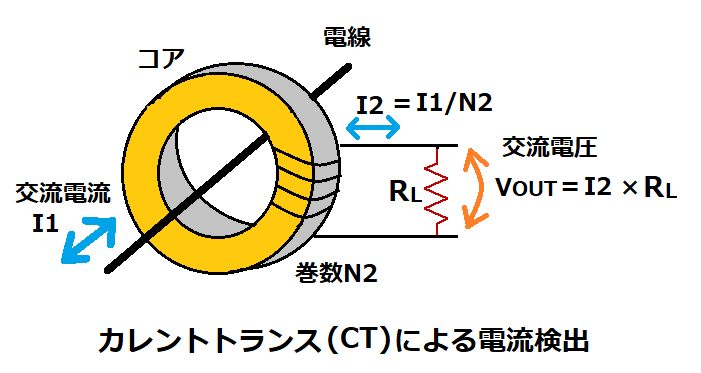
カレントトランス(以下、CT)の構造は一般的なトランスと同じです。
ここで言う一般的なトランスとは入力と出力の関係を電圧で考えるので、
本記事では電圧トランスと称することにします。
電圧トランスの一次側電圧V1と二次側電圧V2は下記式で表現できます。
V1/V2=N1/N2 ・・・(1)
N1とN2は一次側及び二次側の巻数
損失が無い理想トランスの場合、一次側電力=二次側電力なので、
V1 × I1 = V2 × I2 ・・・(2)
I1とI2は一次側及び二次側に流れる電流
(1)と(2)を組み合わせると、
I1/I2=N2/N1 ・・・(3)
(3)式を変形すると
I1=I2 × N2/N1 ・・・(4)
となり、二次側電流I2を測定することで巻数比(N2/N1)より、
一次側電流I1を求めることができ、この(4)式はCTにも適用されます。
次に電圧トランスとCTとの違いについて説明します。
電圧トランスは、できるだけ多くのエネルギーを二次側に伝えるのが目的なので、
一次側電力V1 × I1を大きくするため、一次側コイルに発生する電圧V1が高くなるように
一次側の巻数N1を多くして、一次側インダクタンスL1を大きくしています。(※)
※V1=L1 × di/dtより、L1が大きければV1は高くなります。
一方、CTは、被測定回路のエネルギーをできるだけ消費せずに電流値を計測したいので、
一次側の巻数N1を最小の1ターン(貫通孔に通すだけ)にして、L1を小さくします。
V1が低ければ、I1が大きくても一次側電力V1 × I1を最低限にでき、
CTを挿入したことによる回路での損失を小さくできます。
以上から、(4)式でN1=1とすると下記式になります。
I1=I2 × N2 ・・・(5)
次に、二次側に負荷抵抗RLを接続することで電流I2を検出電圧VOUTに変換します。
VOUT=I2 × RL=(I1/N2) × RL ・・・(6)
しかし、実際のVOUTは若干低くなるため(※)、結合係数Kを用いて以下の様に表現されます。
VOUT=K × (I1/N2) × RL ・・・(7)
※VOUTが理論値より低くなる理由は後述する「CTの精度について」で解説します。
結合係数Kは1以下の値で、メーカーによっては結合係数特性グラフが提示されており、
負荷抵抗RLと一次側(測定)電流I1からK値を読み取ることができますが、
結合係数特性グラフが無い場合は入力電流ー出力電圧特性グラフからK値を算出します。
※各特性グラフについては「CTの使い方」に掲載
・ホール素子を用いる方法
磁界の強さを電気信号に変換するホール素子を使用して電流を検出する方法で、
構造はCTと似ていますが、コアに設けたギャップ間にホール素子を配置し、
コアに通した電線に電流が流れることで発生した磁界によって、
ホール素子から電気信号が出力されます。
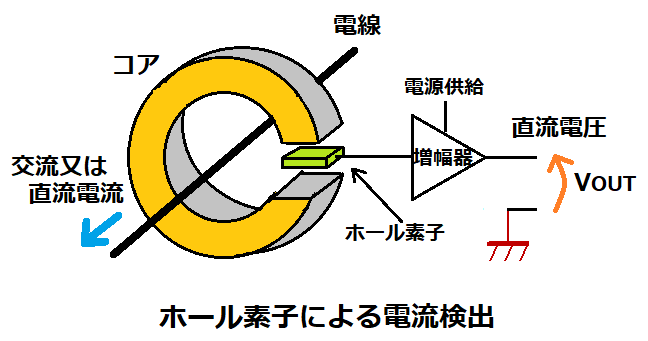
この電気信号は微小電圧なので、オペアンプで増幅されて外部に出力されます。
外観はCTと同様に貫通孔がある貫通型と、
貫通穴が無く、測定電流はピンに接続して計測する非貫通型があります。

CTに比べ、ホール素子による電流検出の感度は低く、
ある程度の大きさの電流が流れないと計測できないことから、
貫通型は数十A程度の大電流か、それ以下の場合は、貫通孔に数ターン巻くなどし、
非貫通型は内部で数ターン巻かれているため、数A以下の電流測定が可能です。
このホール素子を用いた電流検出方法の最大の利点は、
測定対象となる回路とは絶縁した状態で、直流電流も検出できる点であり、
交流電流の検出についてもCTより応答速度が速く、測定精度も高いです。
欠点としては電源供給(単電源又は両電源)が必要であることや、
オペアンプなどの回路が内蔵されているため、コストが高いです。
CTの精度について
CTは外部からの電源供給なしで検出電圧VOUTを出力できますが、
出力に要するエネルギーは電流測定対象となる回路から供給されます。
つまり、CTに流れる一次電流I1の一部を消費してVOUTを出力するため、
実際に流れるI1よりも減少してI2に変換されることで、
VOUTが理想値(=I1/N2 × RL)よりも低下してしまいます。
((7)式の結合係数Kはこの電圧低下の影響を表現しています)
VOUT生成によって一次電流が消費される仕組みについて説明します。
コアに発生する磁束密度B[T]を用いて、VOUT[V]は下記式で表現できます。
VOUT= N2 × ω × B × S ・・・(10)
ω:角周波数=2πf (fは一次電流の周波数[Hz])
S:コアの断面積[m2]
磁束密度Bと磁界の強さH[A/m]との間には以下の公式があります。
B=μH ・・・(11)
μ:透磁率(=μs×μ0)
μs:コアの比透磁率、μ0:真空の透磁率(4π×10-7)
磁界の強さHは一次電流I1[A]と次の関係があります。
H=N1 × I1/ℓ ・・・(12)
N1:一次側の巻数、ℓ:コアの磁路長[m]
CTはN1=1なので、(12)式は以下となります。
H=I1/ℓ ・・・(13)
(10),(11),(13)式を合成すると、
VOUT= N2 × ω × B × S
= N2 × ω × μH × S
= N2 × ω × μ × I1 × S/ℓ ・・・(14)
ここで、fを商用周波数50Hz、N2を1000ターン、Sを10㎜2、ℓを50mmとし、
コア材を珪素鋼板にして、その比透磁率μsを20000とします。
理想的には、測定電流I1が1A流れると、I2は1A/1000=1mAとなり、
負荷抵抗RLを100Ωにした時、VOUT=I2 × RL=100mVとなります。
しかし、実際には(14)式より、VOUTを出力するために消費するI1を計算すると、
I1=VOUT ×ℓ/(N2×ω×μs×μ0×S)
=0.1×50×10-3/(1000×2π×50×20000×4π×10-7×10×10-6)
=0.1×50×1010/(8π2×1010)
=5/(8π2)=0.063A
これを二次電流に換算すると、
I2 = I1/N2 =0.063A/1000=0.063mA
となり、この分だけI2が減少します。
つまり、本来は、I1=1A時にI2=1mAとなるところが、
I2=1mAー0.063mA=0.937mAに減ってしまうことを意味します。
これによって、実際のVOUTは
VOUT = I2 × RL=0.937mA×100Ω=93.7mV
となり、ー6.3mVの誤差が発生します。
RLが小さい方がVOUTも低いため、
消費するI1を減らせることから精度を高くできます。
また、(14)式を見てわかるように、二次巻数N2を増やしたり、
比透磁率μsや断面積Sが大きく、磁路長ℓが短いコアを選ぶことで、
同じVOUTでも消費するI1を減らせるので、精度を向上できます。
上記以外にも、コア巻線の抵抗成分R2による電圧降下(R2 × I2)も、
VOUTを低下させる要因となることから、R2を小さくするため巻線は太い方が良いですが、
それによってコアに巻ける巻数N2が減少してしまうと精度が低下します。
周波数fも高いほど精度が上がりますが、
高周波(数十kHz以上)ではヒステリシス損や渦電流損が増加することから、
コア材については、低周波では珪素鋼板やパーマロイ、
高周波はアモルファスやフェライトが適しています。
CTの使い方
データシートに記載されている以下の特性を基にCTを選定します。
・出力電圧特性
先程説明したように負荷抵抗RLが小さいほど誤差が小さくなるため、
出力電圧特性の直線性が良くなります。
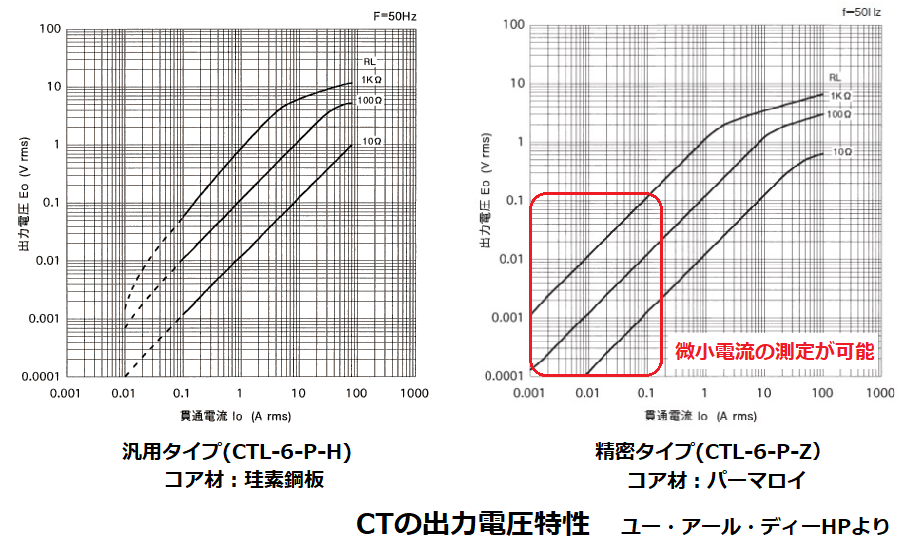
また、パーマロイ等の透磁率μが高いコア材のCTを選ぶことで、
I1(この特性図では貫通電流Io)が微小でも測定が可能となります。
微小電流の測定でVOUTが低くなる場合は、CTの貫通孔に測定電線をNターン巻くことで、
(12)式のN1を1からNに増やすことになり、VOUTをN倍にできます。
・結合係数K特性
(7)式より、Kが1に近いほど理想値に近く(精度が高く)なります。
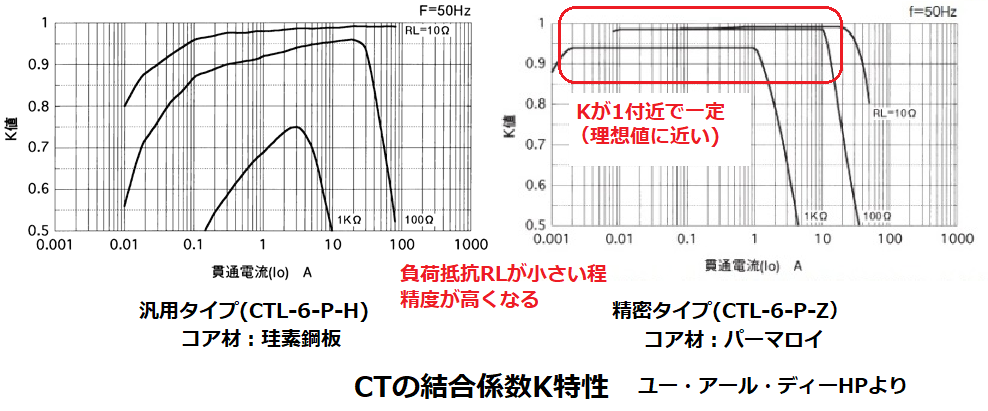
特性グラフを見ると、透磁率が高いコア材の方がKが一定であり、
これによって、上述の出力特性特性の直線性が良いことがわかります。
・周波数特性
低周波領域でのVOUT低下がRLが大きいほど大きくなります。
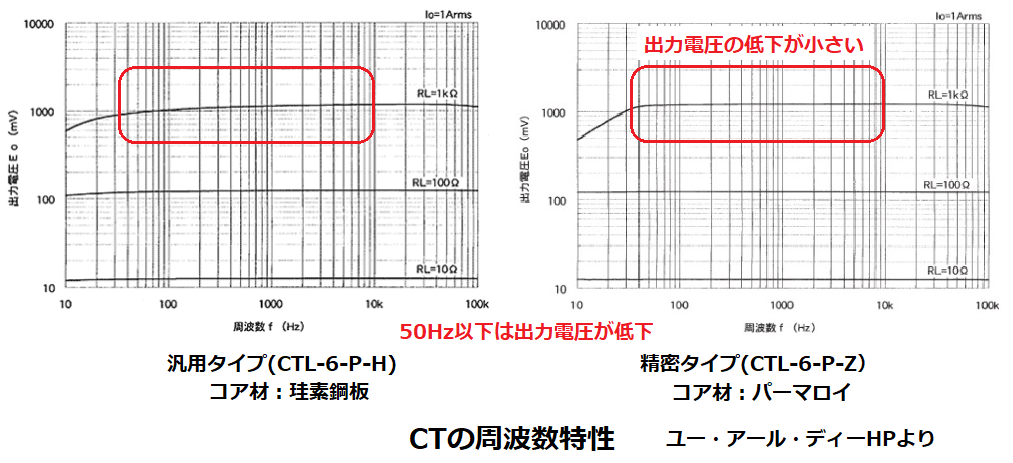
これは(14)式より、周波数ωが下がることで、
VOUT生成のために消費するI1が増加し、その分I2が減少してしまうためで、
この減少量はVOUT(つまり、RL)が大きい程、顕著になります。
記載のCTは商用周波数での使用を前提としているため、
50Hz以下ではVOUTが低下しています。
<CT使用上の注意点>
CTの二次側はオープンにせず、必ず負荷を接続するようにします。
その理由は、オープン状態=負荷抵抗RLが無限大と考えることができるため、
VOUT= I2 × RLより、非常に大きなVOUTが発生することで、
二次巻線が絶縁破壊されて焼損する恐れがあります。
ちなみに、通常の電圧トランスは二次側をオープンにしても問題ないのは、
N2/N1が数百以上のCTと違って大きくないため、VOUT=N2/N1 × V1 より、
V1に比べ、VOUTが非常に高い電圧になることはありません。
CTの二次側に負荷を接続してI2を流すことで、
(2)式(V1 × I1=VOUT × I2)の関係を維持するため、VOUTは高圧になりません。
CTを使った電流検出回路
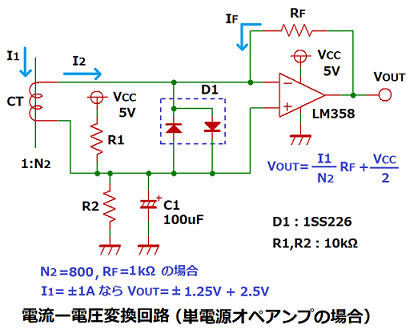
電流ー電圧変換回路
二次電流I2から検出電圧VOUTの生成に負荷抵抗RLではなく、オペアンプを用いる回路で、
CTから見た負荷抵抗が仮想的に0 Ωとなるため精度が高く、周波数特性も良いです。
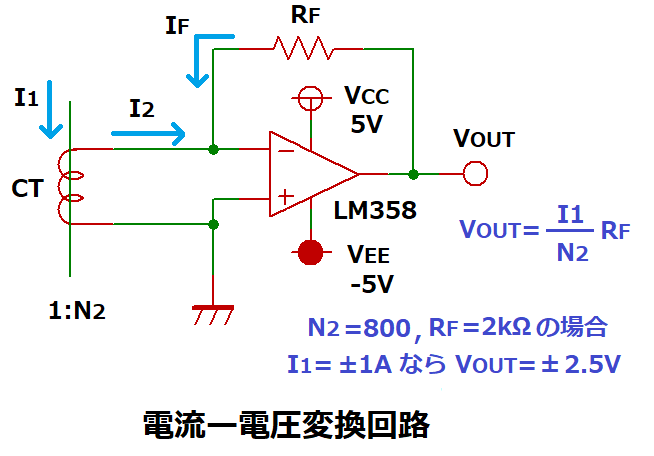
この回路の出力電圧VOUTは下記式で表されます。
VOUT=(I1/N2) × RF
上記式になる理由を説明すると、負帰還(出力がー入力に戻る)構成のオペアンプは、
イマジナリーショート(+入力とー入力は同電圧になる)が適用できるので、
+入力電圧=ー入力電圧となるため、ー端子も0Vです。
ー入力に流れる各電流は下記式で表現できます。
I2=I1/N2、 IF=VOUT/RF ・・・(15)
キルヒホッフの法則(ある地点での電流の総和はゼロ)より、
I2ーIF=0 ・・・(16)
これに(15)式を代入して、
I1/N2ーVOUT/RF=0
これを変形して
VOUT=(I1/N2) × RF
となります。
この回路の特徴は、CTから見た時の出力電圧が0Vであり、
これは、負荷抵抗RL=0Ωと同等であることから、CTの精度が高くなります。
そしてVOUTはRFで決まるので、精度に影響することなくVOUTを大きくできます。
VOUTが±電圧を出力できるように両電源オペアンプが必要です。
この例で使用しているLM358は汎用オペアンプの定番品で、
テキサス・インスツルメンツをはじめ、複数のメーカー品があり、
両電源、単電源どちらでも使用できます。
但し、検出電流が微小な場合には、オフセット電圧(※)の影響が大きくなるので、
OP184(アナログ・デバイセズ製)などの低オフセットタイプを使用します。
※±入力端子に同じ電圧を入力時に理想では出力電圧はゼロとなるが、
実際には内部回路で生じる僅かな入力電圧差のこと。
また、この回路は二次電流I2が数mA程度までの小電流向けになります。
その理由は、一般的にオペアンプは大電流を出力できない(※)ことから、
これが先程の説明で登場した電流IF(つまり、I2)の上限となるため、
これより大きな電流を測定する場合は、後述する電圧増幅回路を使用します。
※LM358の場合で5mA(最悪条件時)
オペアンプの使い方については下記記事で解説しています。
<単電源オペアンプを使用する場合>
電流ー電圧変換回路を単電源オペアンプで構成した回路です。
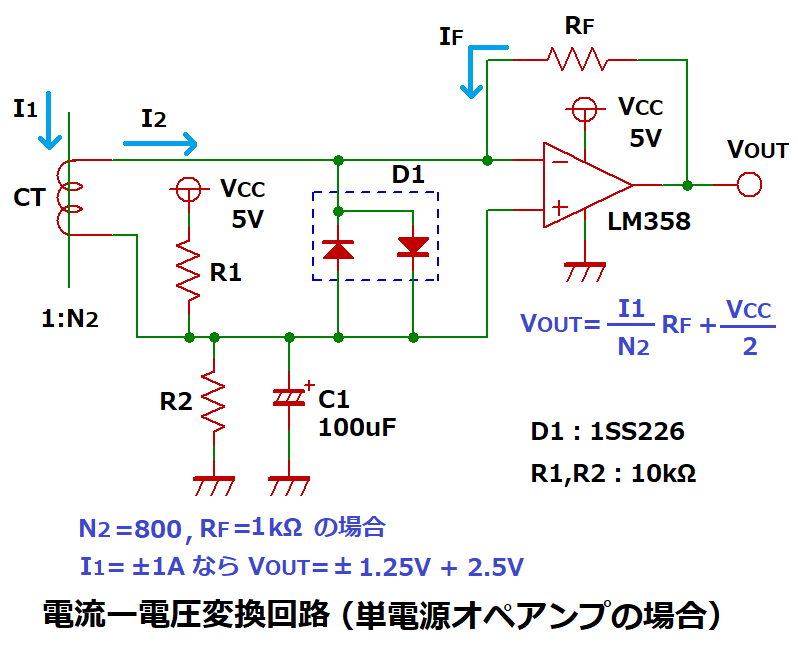
+入力に直流電圧を印加して、VOUTを正電圧のみにシフトさせることで、
単電源オペアンプを使用できるようにしています。
図の様にR1とR2を接続することで±入力ともに電圧がVcc/2になるので、
(15)式の右側の式は下記になります。
IF=(VOUT ー Vcc/2)/RF
従って、VOUTは
VOUT=(I1/N2) × RF + Vcc/2
となり、Vcc/2を中心にした交流波形のVOUTが出力されます。
また、R1やR2をつけたことによる負荷抵抗の影響をキャンセルするため、
コンデンサC1を接続しています。
ここでは、検出電流が50Hz程度の低周波である場合として、
高容量のコンデンサを接続し、交流成分をGNDに短絡させることで
CTから見た時の負荷抵抗をゼロにしています。
D1はオペアンプの入力保護用で、CTに大電流が流れた場合や、
電源VccがOFF時に過大な電圧が入力されないようにします。
ダイオードの選び方については下記記事で解説しています。
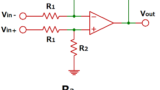
電圧増幅回路
CTに接続した負荷抵抗RLに発生した電圧を増幅して出力する回路です。
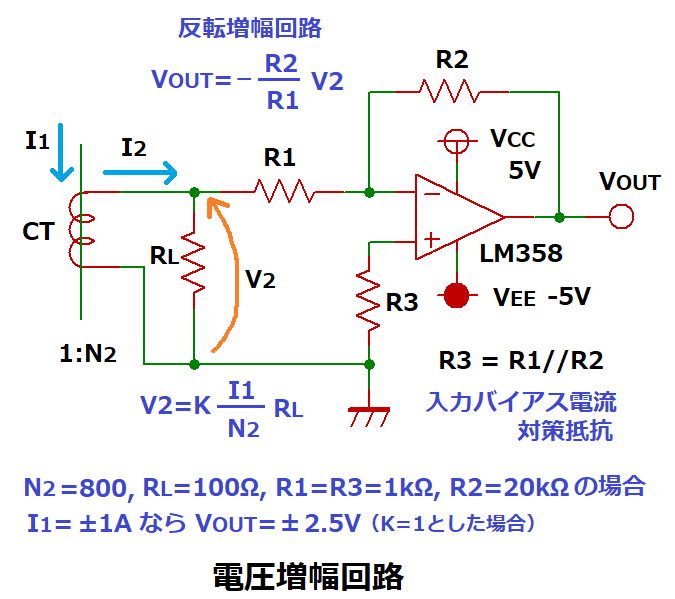
反転増幅回路により、RL間の電圧V2をーR2/R1倍に増幅するため、
検出電圧VOUTはV2と極性が逆になりますが、
交流電圧なので実効値の検出には支障がありません。
反転増幅回路の入力電圧V2は、
V2=K × I1 × RL/N2
となるため、これが増幅された出力電圧VOUTは、
VOUT=ーV2 × R2/R1
=ーK × I1 × RL/N2 × R2/R1
Kは(7)式で説明した結合係数で、CTのデータシートから求めます。
この回路は先述の電流ー電圧変換回路と違い、I2の多くはRLに流れるため、
IFは大きくならず、オペアンプの出力電流が小さくても問題ないことから、
I2が数mA以上となる電流検出に適しています。
R3はオペアンプの入力バイアス電流によるVOUTへの影響を低減するための抵抗で、
R1とR2の並列抵抗値を選択しますが、オペアンプによっては悪化する場合があるため、
まずは反転増幅回路の基本構成(R3=0Ω)で動作を確認した上で、
必要に応じて取りつけます。(本記事最後にある備考を参照)
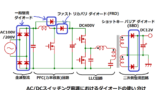
<単電源オペアンプを使用する場合>
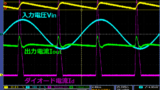
CTの出力をブリッジダイオードで全波整流した電圧をオペアンプに入力することで、
VOUTは正電圧のみになるため、単電源オペアンプが使用できます。
但し、VOUTは実効値ではなく平均値となります。
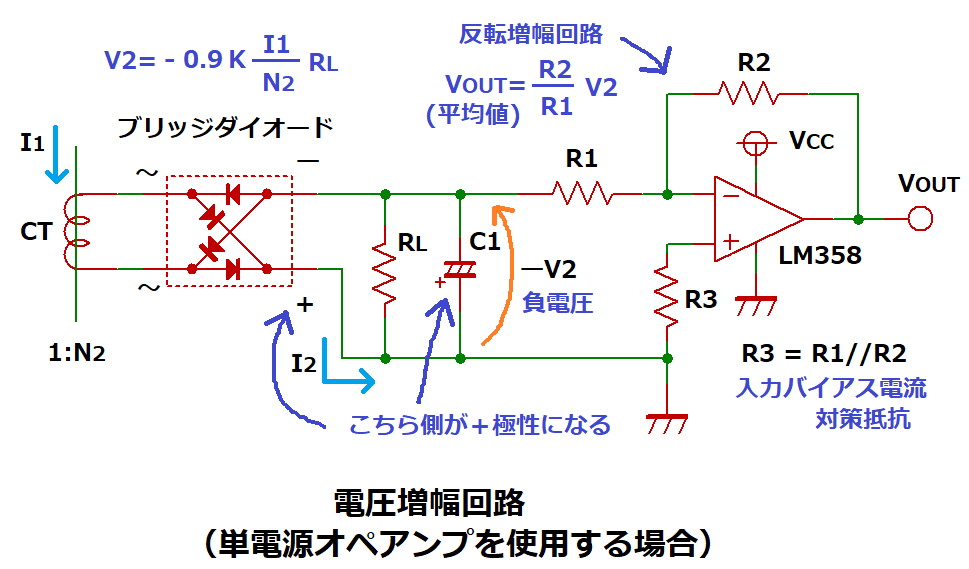
全波整流+コンデンサによる平滑化によりV2は下記式となります。
V2= ー0.9 × K × I1 × RL/N2
0.9は検出電流が正弦波の場合、実効値から平均値への変換定数です。
(ピーク値Vm時の実効値Vm/√2、平均値2Vm/πより、平均値/実効値=2√2/π≒0.9)
マイナスが付いているのは後段の反転増幅回路でVOUTの極性が逆になることから、
ブリッジダイオードのー出力側をV2にしているためです。
従って、出力電圧VOUTは下記式となります。
VOUT= ーV2 × R2/R1
=0.9 × K × I1 × RL/N2 × R2/R1
負荷抵抗RLはブリッジダイオードの出力側に設けることで、
ダイオードの順方向電圧による電圧降下の影響を避けています。
平滑コンデンサCは+極性が下側になるので注意します。
コンデンサ容量の決め方については下記記事で解説しています。
備考:オペアンプの入力バイアス電流による影響について
理想的なオペアンプは入力インピーダンスが無限大なので、
±端子への入力電流はゼロですが、実際には数uA以下の微小電流が流れ、
これを入力バイアス電流と呼んでいます。
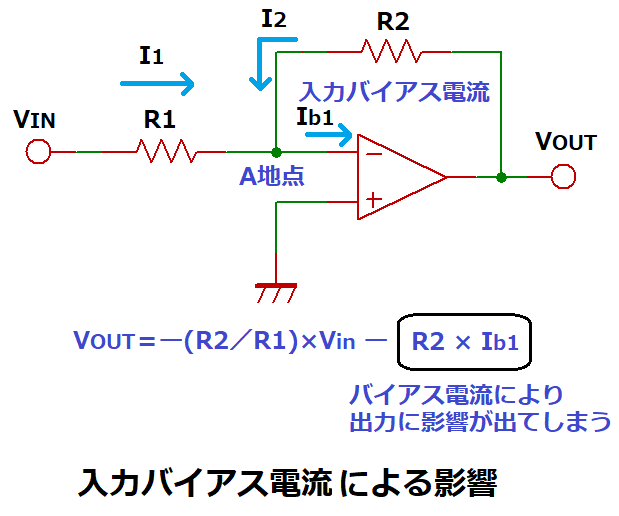
入力バイアス電流による出力電圧への影響を反転増幅回路を例に説明すると、
ー入力への入力バイアス電流Ib1が存在した場合、A地点はキルヒホッフの法則より、
I1+I2+Ib1=0
の関係が成り立ちます。
このA地点は理想オペアンプなら0Vになり、I1=Vin/R1、I2= VOUT/R2となるので、
Vin/R1 + VOUT/R2 + Ib1=0
式を変形すると、
VOUT=ー(R2/R1) × VinーR2 × Ib1
となり、ーR2 × Ib1の電圧降下が発生してしまいます。
仮にIb1が0.5uAと小さくても、R2が100kΩだと50mVの誤差が発生するため、
R2が大きい場合は注意する必要があります。
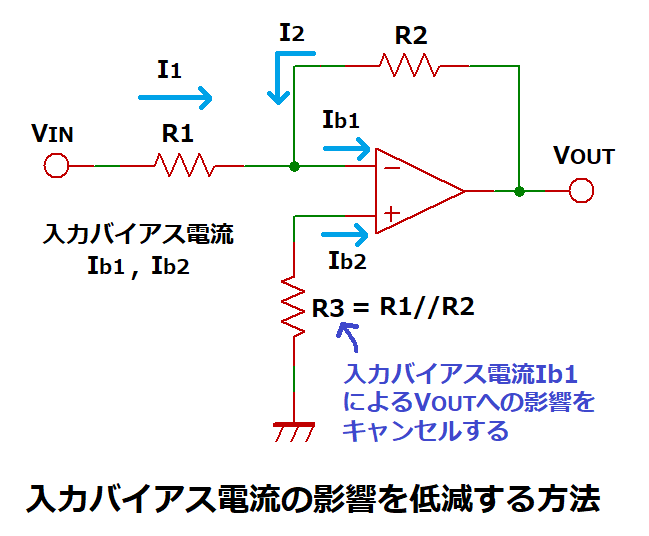
次に反対側(ここでは+端子)にR1とR2の並列抵抗値となるR3を接続することで、
入力バイアス電流の影響を低減できる理由について説明します。
+入力とGND間に抵抗R3を接続した場合、+入力に入力バイアス電流Ib2が流れると
その入力電圧R3 × Ib2は(1+R2/R1)倍(※)されてVOUTに出力されます。
※Vin=0Vとすると、+入力を増幅する非反転増幅回路と考えることができ、そのゲインは(1+R2/R1)となる。
このIb2によって、VOUTに加わる電圧ΔVは下記式で表現できます。
⊿V=R3 × Ib2 × (1+R2/R1)
ここでR3をR1とR2の並列抵抗値とすると
⊿V=R1 × R2/(R1+R2) × Ib2 × (1+R2/R1)
=R2 × Ib2
となります。
ここで±入力の入力バイアス電流が同じ(Ib1=Ib2)なら、
上記VOUTの式にあるーR2 × Ib1と相殺されてVOUTへの影響がキャンセルされます。
(実際にはオフセット電流があるため、完全にはキャンセルされません)
但し、オペアンプの種類によっては、Ib1とIb2で流れる方向が逆の場合もあるため、
R3をつけることで、かえってVOUTへの影響が拡大する恐れがあります。